Exercises

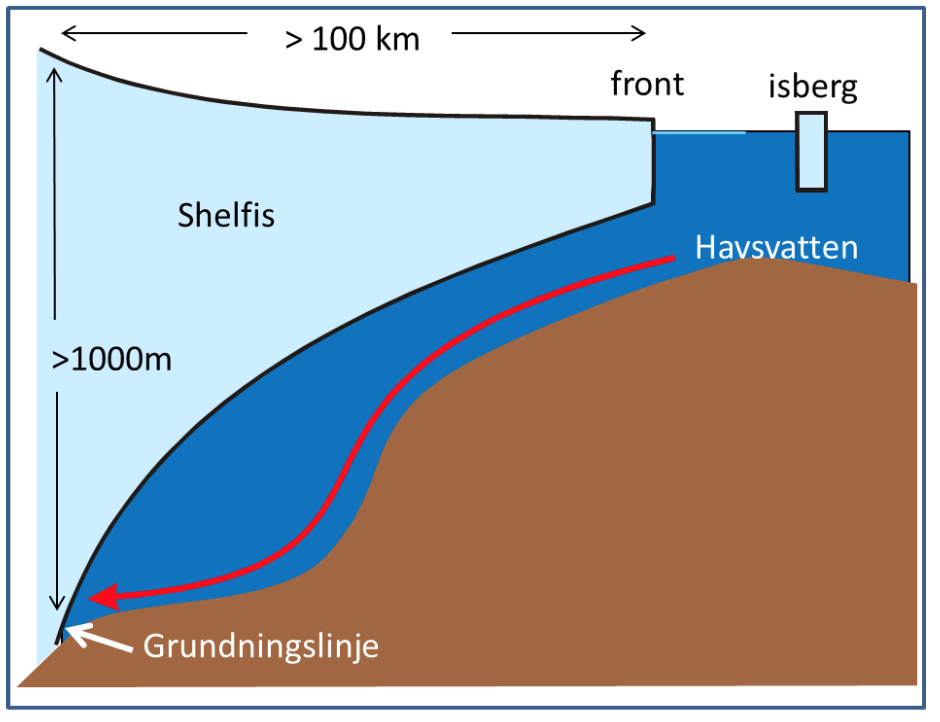
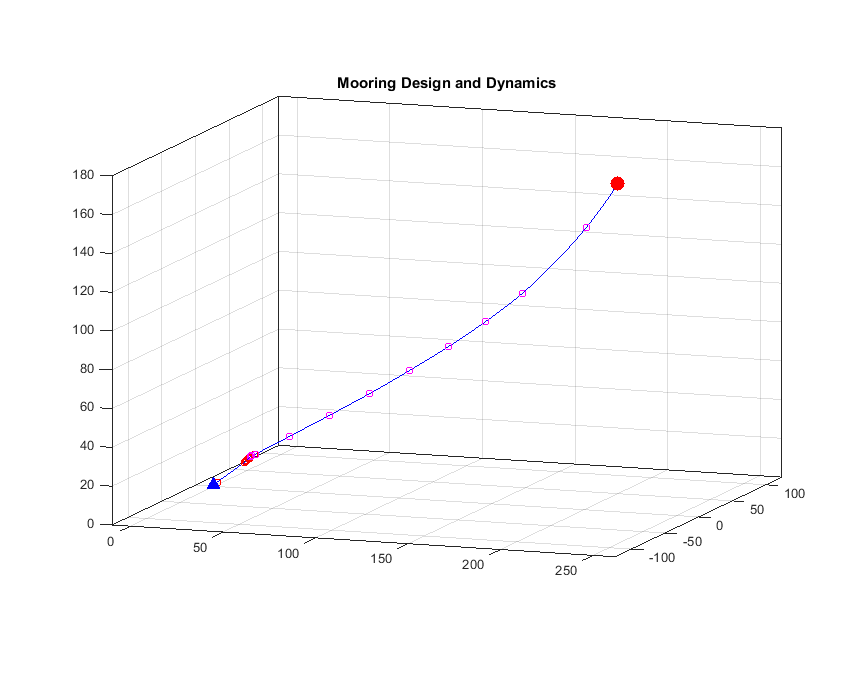
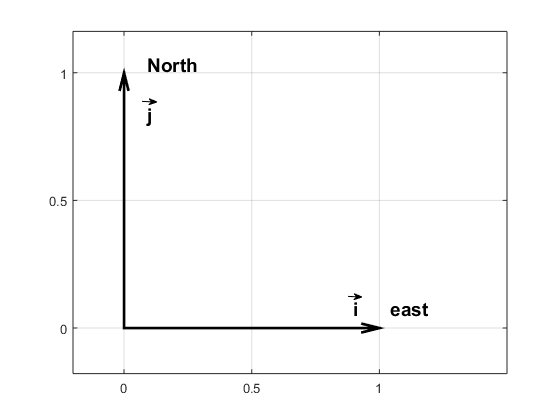
Wind and currents have a strength and a direction and therefor use vectors to represent them, for example: \(\vec{u}=u\vec{i} + v\vec{j}\). \(\vec{i}\) and \(\vec{j}\) are unit vecors pointing towards east and north (see figure) while \(u\) and \(v\) gives the length of the vectors or the strength of the current in that direction If the wind blows towards the north with 10 m/s we have \(\vec{u}=10\vec{i}\); if it blows towards south \(\vec{u}=-10\vec{i}\); and if it blows towards the northeast we get \(\vec{u}=7.1\vec{i}+7.1\vec{j}\).

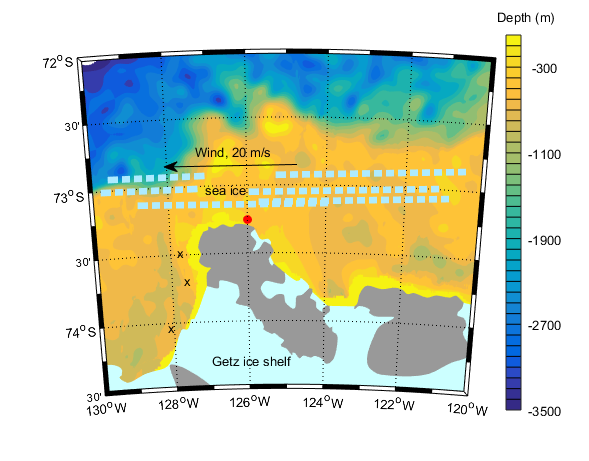
The ice conditions change constantly due to wind and currents – so the captain must follow the evolution through e.g. satellite images so that we don’t get “caught” by the drifting ice. (Araon is an ice breaker, but breaking ice is slow and very fuel consuming) . The sea ice is realtively thin and its motion is most affected by the wind – a rule of thumb is that the ice more with about 2% of the speed of the wind and about 30 degrees to the left of the wind (in the north it moves to the right of the wind).

Exercise 1

The wind is blowing 20 m/s towards the west and the drifting ice is 5 km from land.

a)Express the motion of the wind and the ice on vector format

b) How far southward will the ice move in an hour?

c) How fast does Araon have to drive to make past the peninsula to the moorings on the other side before the ice closes the passage? Will we make it?

Exercise 2

The wind exerts a stress \((\vec{\tau}=\tau_x\vec{i} + \tau_y\vec{j})\) on the sea surface that sets up a current in the water.The size of the stress can be calculated if we know the strength of the wind: \(\vec{\tau}=C_{D}\left|\vec{u}\right|\vec{u}\), where \(\vec{u}=u\vec{i}+v\vec{j}\) is the wind at 10 m height.

1. a) If it is blowing 10 m/s towards the north and \(C_D=1.6\times10^{-3}\), how large is the stress then? In which direction is it acting?
2. b) We know that the size of \(C_D\) change when there is ice on the water and scientist have found that \(C_D=10^{-3}\times(1.5+2.233C_i-2.333C_i^2)\) where \(C_i\) is the fraction of the sea surface that is covered by ice (the ice concentration). For what ice concentration is \(C_D\) largest? smallest? How large was the ice concentration in the exercise above?

Exercise 3

During their expedition on FRAM (1893-1896) the Norwegian oceanographer Nansen observed that the ice was drifting to the right of the wind (he was in the Arctic) and he asked his friend Vilhelm Bjerknes to get one of his students to study the problem. It was the Swedish scientist Vagn Valfrid Ekman who ended up explaining that the motion of ice is an effect of friction and the rotation of the Earth. Ekman developed a theory describing how the current that is set up by the wind behaves. The current changes with depth and we can write: \(\vec{u(z)}=u(z)\vec{i} + v(z)\vec{j}\).

The size of \(u(z)\) and \(v(z)\) can be calculated from the following formaulas (which are not as complicated as they look!)

\(
u(z)=\frac{\sqrt{2}}{1000fd} e^{z/d}\left[\tau_x cos(z/d-\pi/4) -\tau_y sin(z/d-\pi/4)\right]
\)

 

\(
v(z)=\frac{\sqrt{2}}{1000fd} e^{z/d}\left[\tau_x sin(z/d-\pi/4) +\tau_y sin(z/d-\pi/4)\right]
\)

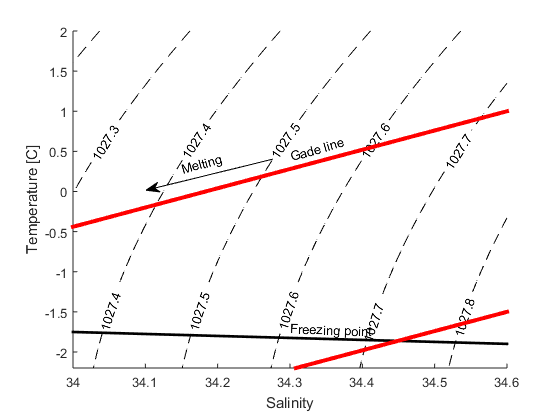
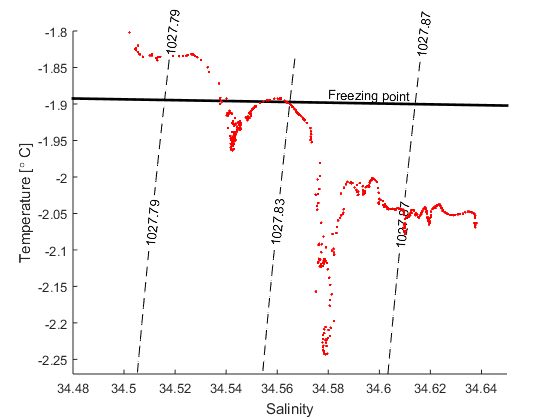
where \(z\) is height (so the depths are negative), \(f=1.46\times10^{-4}sin(latitud)\) is the Coriolis faktorn (caused by the rotation of the Earth) and \(d=\sqrt{\frac{2\nu}{\left|f\right|}}\) is the thickness of the layer that is affected by the wind. We often call this layer the “Ekman layer”. \(\nu=10^{-2}m^2/s\) is the viscosity* – the “thickness” of the water (syrup has a higher viscosity than water**). The theory is well known amongst oceanographers and is referred to as the Ekman spiral.

* The molecular viscosity of water is much lower \(\nu=10^{-6}m^2/s\), but turbulence and eddies make the effective viscosity in the ocean much higher

** see e.g. https://no.wikipedia.org/wiki/Viskositet for an animation showing the effect of viscosity

Exercise 4

1. What is the value of the Coriolis factor in the Amundsen Sea? In Bergen?
2. How thick is the Ekman layer? An iceberg can be several hundred of meters thick – do you think it is affected by the current set up by the wind?
3. If the wind is blowing towards west with 15 m/s and there is no ice – how large is then \(\tau_x\) and \(\tau_y\)? (See exercise 2)
4. In what direction (and with what speed) is the water in the surface (z=0) flowing? At the Ekman depth(z=-d)? At what depth is the current flowing in the opposite direction to the wind?
5. Try to plot the current! Why do you think we talk about an Ekman spiral?
6. When we send down our LADCP*** we get current profiles with a resolution of 8m (i.e we get one measurements for the current every 8 m) Do you think we are able to observe the Ekman spiral? Why/why not?

 

*** the LADCP is an instrument that we send down together with the CTD all the way to the bottom and that measures the current in the water on its way down (and up) so that we get profiles of current in addition to profiles of temperature and salinity.

Exercise 5

 

If you sum up (integrate) the current set up by the wind in the Ekman layer we get the transport, that is how much water that is moved in what direction due to the wind. We often call that the Ekman transport \(\vec{Q_{Ekman}}=U\vec{i}+V\vec{j}\), where

\(U=\frac{10^{-3}}{f}\tau_y\)

 

\(V=-\frac{10^{-3}}{f}\tau_x\)

 

The unit of U and V is \(m^3/m/s\) (or \(m^2/s\)) and they give the amount of water that is flowing by per meter per second. The expression for \(\tau\) is given in exercise 2.

 

1. If it is blowing 15 m/s to the northeast and there is no ice, how larger is then U and V? In what direction is the water transported?
2. How large is the angle between the wind and the transport?
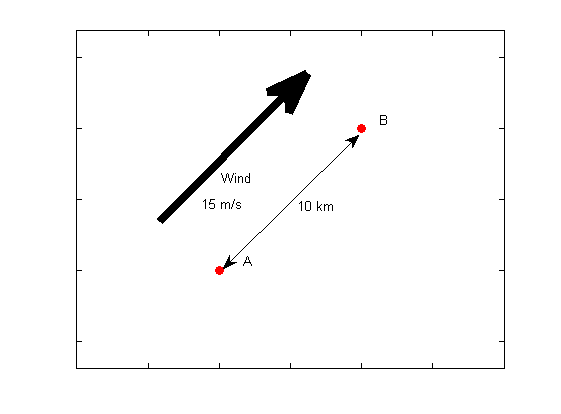
3. We have two buoys (see figure below) that are place 10 km apart and where a line between the buoys are parallel to the wind. How much water flows between the buoys per second? What do you think would have happened I the line between A and B would have been the coast?
4. In what direction do you think the water is blowing when the Bryggen in Bergen is flooded (the tides are also important, off cpurse!)
5. Along the coast of the Antarctic continent the wind is normally blowing towards the west – further north (60S) the wind is blowing to the east. Make a sketch showing the direction of the wind and the Ekman currents. What do you think happens in the middle? Discuss with your friends before reading the answer at the bottom of the page.

 

Convergence and divergence in the ocean

When the wind and thus the Ekman transport changes direction (or magnitude) from one region to another we get “convergence” or divergence. When we have divergence the surface water in an area “disappears” (i.e. it moves away and is not replenished) and new surface water must be provided from below. The water from depth is sucked up to the surface by the wind. In areas where this happens continuously (e.g. around Antarctica) we find large biological activity, since the water from depth is rich in nutrients. If you want to read more, then google e.g. “Wind driven upwelling”.

The freezingpoint of seawater sinks with increasing salinity and with increasing pressure – the more sline the water is, or the higher the pressure is, the more you can cool down the water before it freezes. Water from the tap freezes at 0 0\(^\circ\)C and sea water at -1.9\(^\circ\)C. At 1000m depth you can cool down seawater to -2.6\(^\circ\)C before it freezes. Below the large ice shelves around Antarctica seawater gets in contact with ice at large depths. When water is in contact with ice, it will melt ice and cool down to its freezing point. Below the Filchner-Ronne ice shelf in the Weddell Sea the grounding zone (see figure) is located at 1800 m depth. Here the water can become very cold!

Exercise 1

The freezing point is a function of salinity and pressure \(T_f=T_f(S,P)\). For a constant P (i.e. at one depth level) and for small changes in salinity the freezing point is a linear function of salinity and we can write \(T_f=kS+m\).

a) We know that \(T_f(S=34.4,P=0)=-1.8879^\circ C\) and \(T_f(S=34.7,P=0)=-1.9051^\circ C\). Determine the coefficients \(k\) and \(m\).

b) What is \(T_f(S=34.5,P=0)\)?

c) Vad är \(T_f(S=0,P=0)\)? Is this right? Why/why not??

In a similar manner, we have that (for a given salinity) \(T_f=kP+m\).

d) We know that \(T_f(S=34.5,P=0)=-1.8936^\circ C\) and \(T_f(S=34.5,P=1000dbar)=-2.6466^\circ C\). The pressure increase by about 1 dbar per meter, so the pressure is about 100 dbar at 100 m depth, 200 dbar at 200 m depth and son on. Determine the constants \(k\) och \(m\).

e) What is the freezing point at 2000 m depth?

f) My collegue Svein Østerhus have been drilling through the thick ice on the Filchner-Ronne ice shelf and made observations of the water in the cavity beneath the ice. The lowest temperature they observed was -2.53\(^\circ\)C, the salinity was 34.5. What is the smallest depth the observations can be from?

h) What temperatures could you expect to observe at the grounding line (1800m)

 

Exercise 2

When ice melts in salt water two things happen: the temperature sinks, since the heat from the water is used to melt the ice, and the salinity decreases, since the seawater is mixed with the fresh melt water. To melt a certain quantity of ice we need a certain quantity of heat, if we were to melt twice as much ice, we’d need twice as much heat. The change in temperature is proportional with the change in salinity \(k=\Delta T/\Delta S\)=2.4. A line with a slope of 2.4 in a TS-diagram (a diagram with salinity on the x-axis and temperature on the y-axis) shows how the the salinity and temperature changes when ice is melting in seawater. It is called a “Gade line” (see figure below) after professor H. Gade at UiB.

a) Find the equation (\(T=kS+m\)) that describes how the temeprature and salinity changes when ice is melting in water with T=2\(^\circ\)C and S=34.6? Plot the line in a TS-diagram.

b) How salty is the water when T=0\(^\circ\)C?

c) How saline is the water when it is at its freezingpoint? Here you’ll need to use the expressin for the freezingpoint that you found in exercise 1 (P=0)

d) The figure below shows a TS-diagram with data from a CTD station  (ENG_Filchner_CTD)  that was occupied at the front of the Filchner ice shelf when I was there a few years ago. What was the lowest temperature we observed? How saline was that water?

e) Find the expression for the Gade line that goes through the T,S point from (d) and plot it together with the data and the line that gives the freezing point (from exercise 1, P=0)

f) Most of the water entering the Filchner cavity is at its surface (P=0) freezing point. How saline was the coldest water thtat we observed when it entered the cavity, that is, before it melted ice?

Using the Gade line we can determine how saline the water that exit the cavity was when it entered the cavity. Since we know how the salinity changes along the front of the ice shelf (it increases the further west you go) we can also determine where the water entered the cavity

 

We go on scientific expeditions to the Amundsen Sea every other year or so, and then we do a lot of measurements and learn what things are like right then, when we are there. But we’d off course want to know also what happens when we are not around. To do so we deploy “moorings”. A mooring is and anchor, a line on which we attach instruments and floating elements to keep it upright in the water. The moorings are standing on the bottom and measures (normally currents, salinity and temperature but I’ll also have sensors to measure the concentration of oxygen) until we return a year or two later. What the mooring looks like and what instrument we put on it will depend on what we want to measure. At the bottom of the page there is a drawing of one of my moorings!

Exercise 1

Now you can design you mooring! What would it look like if you’d want to:

a) Study the evolution (salinity and temperature) of the surface layer (let’s say the upper 200 m) over a year in a area where the water is 500 m deep?

b) Study a bottom current that extends 300 m above the bottom

c) Find out how much warm water is entering the cavity below an ice shelf. The depth is 800 m and the draft of the ice shelf is 300 m deep (which means that ice bergs can reach just as deep!!)

 

Exercise 2

Do the following calculations for you mooring from above or for a mooring which has

1 x acoustic release (25 mab); 3 X SBE37 (25, 150 and 300 mab), 1 x RCM (50 mab) 1 x ADCP (300 mab) and 5 x SBE56 (50, 75, 100, 200, 250 mab). Mab = meters above bottom.

The instrument has the following dimensions (they are all roughly equal to cylinders)

a) What is the weight of all the instruments in air? In water?

The mooring also needs floating elements to stand up in the water.

b) How much can one glass sphere lift? Their diameter is 43 cm and the weigh 22 kg in air.

c) How many spheres do we need to keep the mooring up right?

Exercise 3

When the current is strong it will tend to pull the mooring down towards the bottom – that is not good. Firstly, you don’t get measurements from the depth you wanted and secondly, many of the instrument cannot measure when they tilt too much, An ADCP, for example, cannot measure correctly if the tilt is above 15 \(^\circ\). So we need to add extra floating elements to make sure that the mooring is not pulled down if the current is strong. The force from the water pulling the mooring down is proportional to the area that the water hits (i.e. the cross sectional area of the mooring).

a) What percentage of the mooring cross sectional area is made up by the rope?

b) By how much is the area reduced if we change for a line that is 6 mm in diameter?

c) An instrument was pulled down to 170 mab and 218 m downstream, another instrument was pulled down to 65 mab and 105 m downstream. The shape of the line can be decribed by (half) a parable. Find the expression for the parable!

d) The pressure sensor on the ADCP shows that it now is 40 mab. How much is it tilting? Can we use the measurements?

e) How high up must it be (at least) for the measurements to be good?

f) Why do you think we prefer to have the ADCP high up looking down, rather than deep down looking up?

Exercise 4

When we retrieve the mooring and download the data from the instruments we get time series of current, temperature and salinity. We will now do some calciulations based on data from a mooring that was deployed in the Amundsen Sea in 2012.

a) Import and plot the current measurements from mooring S4, 17-24 June 2012 (ENG_Riggdata_S4_1). Describe what you see!

b) What is the mean current? In what direction was the water flowing? (\(u\) is the current in the \(x\)-direction (towards the east) and \(v\) is the current in the \(y\)-direction (towards the north))

c) If you were to describe the observations with a mathematical function, which one would you chose?

d) Determine the coefficient of your function!

e) An iceberg is floating with the current in the vicinity of S4. Set up an expression for it movement (using vectors) and plot its trajectory. How would you describe its movement?

f) Plot the current a week forward in time using your function from (d).

g) Import the data from S4 24/6-1/7 and plot it in the same figure. Is your model doing a good job predicting the currents? Why? Why not? (The file is named ENG_Riggdata_S4_2)

 

Exercise 5

Import and plot the measurements of pressure from mooring C2. The file is named ENG_Riggdata_C2. In this location the currents were much stronger than we expected and we had put on too little flotation 🙁

a) How would you interpret the record? (hint – look at exercise 2 above)

b) At what depth is the instrument located when the current is weak? (1 m \(\approx\) 1 dbar)

c) How deep is it pulled down?

d) What percentage of time is it pulled down more than 40 m? 80 m?

e) \(u\) gives the current in the \(x\)-direction (towards the east) and \(v\) gives the current in the \(y\)-direction (towards the north). Set up an expression for the current strength the calculate and plot it! How strong is the strongest current? The mean current? How many km/h is that?

f) Is there a relation between current strength and pressure (that is, the instrument pull- down?) Describe the relation mathematically and with words.

Exercise 6

The instruments are powered by batteries, and every time we make measurements we use a small amount – or a lot if it is an ADCP – energy. We want the instruments to keep measuring until we get back to pick them up – so we have to calculate beforehand how often we can make measurements without emptying the battery. But we also have to think about e.g. tides when determining how often to sample.

a) One of the components of the daily tides has a period of 25.8 h. The tidal current can be described by a sinus curve. The amplitude (and the phase) depends on where we are, but let’s assume the amplitude is 10 cm/s and the phase is 0. Set up an expression for the tidal current and plot it for 30 days.

b) If we made measurements only once a day, what would or time series look like?

c) What is the period of the “oscillation” that we would then observe?

d) The tidal current tha we observe is the sum of many components with different periods, amplitudes and phases. Another component has a period of 23.93h. Set up an expression for that tidal component if the amplitude is 9 cm/s. (You can set the phase to 0) and plot the sum of the two components. What do you see? How is the amplitude changing? How far is it between to “amplitude maximum”? Can you explain what you see? (hint: plot the components as well as the sum of them). Compare the results with the results from exercise 3!

Oceanographers like me often talk about «water masses», that is water with different origin that therefore has different salinity and temperature. We talk about “Atlantic water”, which is warm and salty, about Antarctic surface water which is fresh and col or about Antarctic shelf water which is cold and salty. The salinity and temperature of the water will determine its density; cold water is denser than warm water, fresh water is lighter than saline water.

The properties of the water masses are to a large extent set by the atmosphere. Where it is warm, the water is heated up and where it is cold the water is cooled down. The salinity is determined by evaporation, freshwater input (from rivers or precipitation) and by the formation of sea ice. When ice is formed during the winter, it is the water molecules that freeze. Most of the salt is rejected, and the salinity in the water below the ice thus increases. In shallow areas where a lot of ice is formed – for example in some parts of the continental shelf surrounding Antarctica – the water can become very saline and hence very dense.

The exercise below is about Circumpolar Deep Water, CDW. CDW is actually a mixture of several water masses, amongst other water that orinates as far away as the North Atlantic. CDW has a temperature between 1-2 degrees and a salinity between 34.62 and 34.73. Strangely enough, salinity does not have any unit, but is approximately permil so if the salinity is 1 there is about 1 gram of salt per kilo water. The salinity in the ocean is typically about 35, or 3.5%.

In a TS-diagram (a graph with salinity on one axis and temperature on the other axis, see below) a water mass is a point or a small box – if we mix two water masses the mixture will lie on a straight line between the two water masses.

Exercise 1

You have two bottles A and B where \(S_A\)=33.2, \(T_A\)=4C and \(S_B\)=34.8, \(T_B\)=1C. Mark them in a TS-diagram

1. What is the salinity and temperature of a mixture that is made of 50% A and 50% B?
2. What is the salinity and temperature of a mixture that is made of 10% A and 90 % B?
3. What is the salinity and temperature of a mixture that is made of 73% A and 27% B?
4. Plot your mixtures in the TS-diagram. What do you see?
5. If you have a third water mass \(S_C\)=33.7, \(T_A\)=0C – which mixtures can you get then?

Exercise 2

Import and plot salinity and temperature from the mooring S4, 320 m depth as a function of time (the file is named ENG_Riggdata_S4_TS).

1. Time is given as days since 1 january, 2012. What day was the mooring deployed? Recovered?
2. What is the average temperature /salinity and standard deviation?
3. Is there a seasonal signal? Can you describe it with a sinus function? Why / why not?
4. Plot temperature versus salinity in a TS-diagram – what do you see? Can you describe the relationship between salinity and temperature with a linear regression?
5. An instrument in the vicinity of the mooring measured S=34.25, S=34.6 and S=33.9. What do you think the temperature was?
6. Are your answers to the exercise above reasonable? Sea water freezes at -1.9C. For what salinities are your regression valid?
7. The observations show that the mooring is surrounded by a mixture of CDW (Circumpolar Deep Water) and WW (Winter Water). What are the salinity/temperature of our CDW? WW normally has a temperature of -1.9C. Do we observe pure WW at our mooring? Use your regression to determine the salinity of the WW.
8. You now have determined the properties (S and T) of WW and CDW. What is the temperature and salinity in a mixtruer of 10% CDW and 90%WW? 75% CDW abd 25% WW?
9. What would be the termeprature of water with a salinity of 34.45? What fraction of the water is CDW?

Exercise 3

The density of seawater depends on its salinity and temperature. Cold water is denser than warm fresh water is lighter than saline water. The relationship between S, T and density is complicated, but for small changes in salinity and temperature the relationship is approximately linear.

\(   \rho = \rho_0 [1 + \beta (S – S_0) – \alpha (T – T_0) ] \)

In the expression above \(S\) is salinity, \(T\) is temperature, \(\beta\) is the haline coefficient and \(\alpha\) is the thermal coefficient. \(S_0\) och \(T_0\) are reference values that you can choose freely and \(\rho_0=\rho(S_0,T_0)\). The values of \(\alpha\) and \(\beta\) depends on what values you chopse forr \(S_0\) and \(T_0\). If we chose \(S_0\)=34.6 and \(T_0=\)=0.5C then \(\rho_0=\rho(S_0,T_0)\)=1027,8 kg/m\(^3\), \(\alpha \approx \) 5.77*10\(^{-5}\) C\(^{-1}\) and \(\beta \approx 7.84*10^{-4}\).

Use the linearisation to calculate density profiles based on the temperature and salinity profiles from the Amundsen Sea (file ENG_CTDdata_Amundsenhavet). What do they look like compared with the salinity and temperature profiles?

1. Chose one of the profiles? Where is the density largest? Smallest? Why is it like that?
2. How big is the density difference between the bottom and the surface? How much more saline must the water in the surface be to be as dene as the water at the bottom?
3. The density must increase with depth, otherwise the water column I unstable: dense water is lying on top of light water. The dense water then will sink down to “its” level (this is called convection)
4. If we cool down the water in the surface to the freezing point (-1.9C), what will happen?

Strong wind can mix the upper layer so that we get a homogenous layer (constant salinity and temperature). The salinity is then equal to the mean salinity.

1. What is the mean salinity of the upper 100 m?
2. How heavy would the homogenous surface layer be if it was cooled down to the freezing point (-1.9C)
3. By how much do we have to increase the salinity for the water in the surface to be as heavy as the water at the bottom? (How can this happen in Antarctica? In the Mediterranean Sea?)

 

Exercise 4

When the temperature increase the density decrease – that means that1 kg of warm water occupies a larger space than 1 kg of cold water. A large part of the sea level rise that we are observing today (and that we will see in the future) is caused by the increase in temperature of water at depth in the ocean. If water which is 4000m deep (with \(S_0\), \(T_0\), \(\rho_0\),\(\beta\) and \(\alpha\) as given in exercise 3) is heated by 1C, how much will the sea level then rise?

Exercise 5

It is the water molecules that forms crystals when sea water freezes – the salt is rejected by the growing ice and mixes with the sea water below. The salinity* of freshely frozen ice is typically 7-10**. Since the salinity has such a large influence on the density, we want to find out how much the salinity in the water increases (\(\Delta S\)) when ice of a certain thickness (\(h_{ice}\)) and salinity (\(S_{ice}\)) is formed. We can do that using the formula:

\(\Delta S= \frac{h_{ice}(S-S_{ice})}{H_{water}}\) where \(H_{water}\) is the thickness of the layer that the salt mixes into.

1. By how much does the salinity increase of we freeze (i) 10 cm (ii) 1 m of ice over a 100 m thick layer where S=34.5 and \(S_{ice}\) =7?
2. By how much does the salinity increase of we freeze (i) 10 cm (ii) 1 m of ice over a 1000 m thick layer where S=34.5 and \(S_{ice}\) =7?
3. By how much does the density increase in a-b? (Set T=T\(_f\) (See exercize 3).
4. How much ice do we have to freeze for the water in 3h to be as heavy as the water on the bottom? (Let H=100 m, the thickness of the layer that the storm mixed) Is that realistic?

*You determine the salinity of ice by melting it down and measureing the salinity of the melt water.

**For old ice in the Arctic the salinity can be almost zero!

 

The ice shelves in the Amundsen Sea are melting relatively quickly since warm water is entering the cavity beneath the ice. We thus want to know how much heat the water on the continental shelf contains, and how much heat that is entering the ice shelf cavity. The heat content is given relative to a reference temeprature \(T_{ref}\). What you calculate, is how much heat you have to remove before the temperature of the water is \(T_{ref}\). If you have to add heat for the water to reach \(T_{ref}\), then the heat content is negative.

We can find the heat content \(H\) in the water from a CTD-profile (observations of temperature, and salinity from the surface to the bottom):

\(H\approx\sum_{z=1}^{depth}\rho c_p \left(T(z)-T_{ref}\right)\Delta z\)

\(\rho\) is the density of the water (about 1027 kg/m\(^3\) and \(c_p=4\times10^3\)J/kg/C is its heat capacity.

You are free to choose the reference temperature – but since sea water freezes and -1.9C it is practical to choose \(T_{ref}\)=-1.9C. The heat content is then the energy one can remove from the water before it freezes. \(H\) is the heat conent per square meter.

When warm water is in contact with ice the heat will be used to melt ice. To melt a kilo of ice you need approximately 330 kJ (or a bit more if the ice is cold).

Exercise 1

1. Import the data from the CTD-profiles from the Amundsen Sea (you’ll find them one after each other in the file ENG_CTDdata_Amundsenhavet in Geogebra. Plot a few of the profiles and calculated the heat content
2. How much of the heat is found in the upper 200 m? below 200 m depth?
3. We are mostly interested in the heat at depth. Do you know why?
4. Make a table where you note the heat content (in the upper and lower layer separately) and the temperature at the bottom. (You may well cooperate in groups!)
5. My colleagues argue that there is a direct relationship between the bottom temperature and the heat content, so that all we’d need to measure is the temperature at the bottom. What does it look like in your data? Can you draw a conclusion based on the data at hand? Discuss!

If you want to add more points to your table, you can download data from the entire cruise in 2010 from NODC, a large data bank where we scientist send our data so that other researchers (and you!) can use them!

Exercise 2

1. How much ice (per square meter) can we melt with the heat from the profiles above?
2. The melt below the ice shelf in the Amundsen Sea is about 400 Gton per year. How much heat is that?

Exercise 3

1. If the West Antarctic Ice sheet were to collapse, the sea level would increase with three meters – how many cubic meters of ice does that correspond to?
2. How much heat is needed to melt that ice? (Does it have to melt for the sea level to rice?)
3. A wind turbine typically produce 2 MW – how long time would it take for the wind turbine to produce the energy needed to melt the ice?
4. The earth receives about 0.5 W/m\(^2\) more energy (through radiation) from the sun than what is given off – how long time would it take to melt the ice if all of the energy was used to melt ice?
5. A Norwegian uses about 30 000 kWh per person per year –how many cubic meters of melted ice does that correspond to?

[slr-infobox]
Radius of the Earth: 6371 km

Density, ice: 900 kg/m\(^3\)

Density, snow: 900 kg/m\(^3\)

Density, sea water: 1027 kg/m\(^3\)

Percentage of the Earth that is water: 70%
[/slr-infobox]

Ice, ice, ice! There is sea ice everywhere! Large floes, small floes and the odd iceberg. It is all white, and all beautiful, and it puts a definitive end to waves and seasickness!

When heat is removed from water, the water will cool and it will continue to do so until it reaches its freezingpoint. If we continue to remove heat, the water will freeze. The heat that we remove is then the latent heat. Normally it is not “we” who remove heat, but the atmosphere. When the air above is colder than the ocean below, heat will move from the water up into the air: the colder it is, the faster the heat moves. That is, the colder it is, the faster the ice grows. But the ice is a good isolator; it will isolate the water from the cold atmosphere above. Just like your jacket isolates you when it is cold outside and makes you keep the warmth inside, the ice causes the water to loose heat more slowly, since the heat must be conducted through the ice in order to be lost to the atmosphere. The thicker the ice is, the more slowly is the heat conducted through the ice, since the heatflux (\(F_{ice}\), i.e. the amount of heat that is conducted through the ice per unit of time) is proportional to the temperature gradient:

\(F_{ice}=-k_{ice}\frac{dT}{dz}=-k_{ice}\frac{T_{atm}-T_{f}}{H}\)

\(k_{ice}=2\,W\,m^{-1}\,^{\circ}C^{-1}\) is the heat conductivity of ice and \(H\) is the thickness of the ice.

\(T_{atm}\) is the temperature at the top of the ice (which we assume to be equal to the temperature of the air) and \(T_f=-1.9^\circ C\) is the temperature at the bottom of the ice, that is, the freezingpoint of sea water.

The latent heat that is released (per square meter) when the ice is growing a little bit\(dH\) is \(\rho_{ice}LdH\). If that happens during a short time \(dt\), then the latent heat flux is:

\(F_{latent}=\rho_{ice}L\frac{dH}{dt}\)

 

\(\rho_{ice}=900\,kg\,m^{-3}\) is the density of ice and

\(L=3.3*10^5J\,kg^{-1}\) is the latent heat of fusion.

The ice will grow exactly as fast as the latent heat can be conducted up through the ice, i.e. so that

\(F_{latent}=F_{ice}\)

When combining the two equations we get a differential equation, that we can solve to get an expression for how the ice thickness increase in time, \(H(t)\).

Exercise 1

a) Set up the differential equation and show that the solution \(H(t)\) is

\(H=\sqrt{ H_0^2+\frac{2k_{ice}(T_{f}-T_{atm})}{\rho_{is}L}t}\).

when \(H(t=0)=H_0\)

Hint: Use the chain rule \(\frac{dH^2}{dt}=2H\frac{dH}{dt}\).

b) Let \(H_0=0\) and plot the function for different \(T_{atm}\)!When does the ice grow fastest? Why?

c) Use the equation from (a) to calculate the thickness of the ice ten hours after it started freezing if the temperature outside is (i) -20C (ii) -2C.

d) When the ice is 1 m thick, how long is it before it grow another 10cm?

e) What do you think will happen if there is snow falling on the ice? \(\kappa_{\textit{snow}}\) is typically between 0.15 and 0.4\(W\,m^{-1}\,^{\circ}C^{-1}\). What is the better isolator? Snow or ice?

f) All heat that is conducted up through the ice has to be conducted through the snow as well. Where is the temperature gradient largest? In the snow or in the ice? Make a sketch!

Exercise 2

The temperature varies from day to day and from year to year. The file ENG_Temperatur gives temperature data from the Amundsen Sea from March 2014 to March 2015.

a) Find the mean temperature for each month and plot it. Find the standard deviation and add it to your graph. What month is coldest? Warmest? When is the temperature most variable?

b) When does the ice stop to grow?

c) Find out how much the ice thickness increase everyt month? What value should you use for \(H_0\)?

d) Plot the (i) the ice thickness and (ii) the ice growth as a function of time. When is the ice growing fastest? Is this when it is coldest? Why? Why not?

Exercise 3

1. If an ice flow is 30 cm thick, 2 m wide and 5 m long – how much of the ice floe is then above water? \(\rho_{ice}=900kg m^{-3}\)
2. How many scientist can stand on the ice flow (in the middle)without getting their feet wet?
3. How much snow can fall on the ice before the ice floe is submerged? \(\rho_{snow}\approx 300kg m^{-3}\)

Exercise 4

The ice in Antarctica is relatively thin and it often snows so much that the ice is submerged. Then we’ll have a layer of slush (snow + seawater) on top of the ice. When the slush freezes, we get what is often called “snow ice”. Estimations suggests that as much as 40% of the ice in the Amundsen Sea is snow ice!

1. It is quicker to freeze snow ice than regular sea ice – can you explain why? How far does the heat have to be conducted when freezing snow ice? Does the snow have to freeze?