English

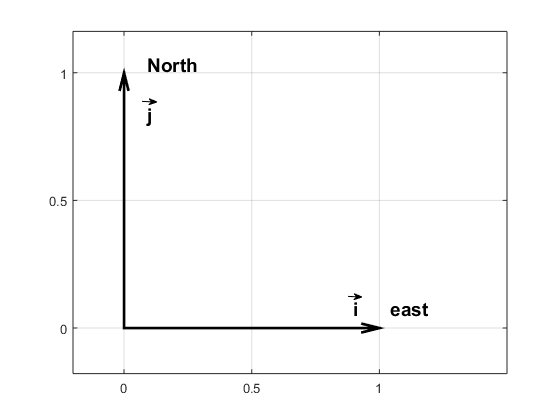
Wind and currents have a strength and a direction and therefor use vectors to represent them, for example: \(\vec{u}=u\vec{i} + v\vec{j}\). \(\vec{i}\) and \(\vec{j}\) are unit vecors pointing towards east and north (see figure) while \(u\) and \(v\) gives the length of the vectors or the strength of the current in that direction If the wind blows towards the north with 10 m/s we have \(\vec{u}=10\vec{i}\); if it blows towards south \(\vec{u}=-10\vec{i}\); and if it blows towards the northeast we get \(\vec{u}=7.1\vec{i}+7.1\vec{j}\).

The ice conditions change constantly due to wind and currents – so the captain must follow the evolution through e.g. satellite images so that we don’t get “caught” by the drifting ice. (Araon is an ice breaker, but breaking ice is slow and very fuel consuming) . The sea ice is realtively thin and its motion is most affected by the wind – a rule of thumb is that the ice more with about 2% of the speed of the wind and about 30 degrees to the left of the wind (in the north it moves to the right of the wind).

Exercise 1

The wind is blowing 20 m/s towards the west and the drifting ice is 5 km from land.

a)Express the motion of the wind and the ice on vector format

b) How far southward will the ice move in an hour?

c) How fast does Araon have to drive to make past the peninsula to the moorings on the other side before the ice closes the passage? Will we make it?

Exercise 2

The wind exerts a stress \((\vec{\tau}=\tau_x\vec{i} + \tau_y\vec{j})\) on the sea surface that sets up a current in the water.The size of the stress can be calculated if we know the strength of the wind: \(\vec{\tau}=C_{D}\left|\vec{u}\right|\vec{u}\), where \(\vec{u}=u\vec{i}+v\vec{j}\) is the wind at 10 m height.

1. a) If it is blowing 10 m/s towards the north and \(C_D=1.6\times10^{-3}\), how large is the stress then? In which direction is it acting?
2. b) We know that the size of \(C_D\) change when there is ice on the water and scientist have found that \(C_D=10^{-3}\times(1.5+2.233C_i-2.333C_i^2)\) where \(C_i\) is the fraction of the sea surface that is covered by ice (the ice concentration). For what ice concentration is \(C_D\) largest? smallest? How large was the ice concentration in the exercise above?

Exercise 3

During their expedition on FRAM (1893-1896) the Norwegian oceanographer Nansen observed that the ice was drifting to the right of the wind (he was in the Arctic) and he asked his friend Vilhelm Bjerknes to get one of his students to study the problem. It was the Swedish scientist Vagn Valfrid Ekman who ended up explaining that the motion of ice is an effect of friction and the rotation of the Earth. Ekman developed a theory describing how the current that is set up by the wind behaves. The current changes with depth and we can write: \(\vec{u(z)}=u(z)\vec{i} + v(z)\vec{j}\).

The size of \(u(z)\) and \(v(z)\) can be calculated from the following formaulas (which are not as complicated as they look!)

where \(z\) is height (so the depths are negative), \(f=1.46\times10^{-4}sin(latitud)\) is the Coriolis faktorn (caused by the rotation of the Earth) and \(d=\sqrt{\frac{2\nu}{\left|f\right|}}\) is the thickness of the layer that is affected by the wind. We often call this layer the “Ekman layer”. \(\nu=10^{-2}m^2/s\) is the viscosity* – the “thickness” of the water (syrup has a higher viscosity than water**). The theory is well known amongst oceanographers and is referred to as the Ekman spiral.

* The molecular viscosity of water is much lower \(\nu=10^{-6}m^2/s\), but turbulence and eddies make the effective viscosity in the ocean much higher

** see e.g. https://no.wikipedia.org/wiki/Viskositet for an animation showing the effect of viscosity

Exercise 4

1. What is the value of the Coriolis factor in the Amundsen Sea? In Bergen?
2. How thick is the Ekman layer? An iceberg can be several hundred of meters thick – do you think it is affected by the current set up by the wind?
3. If the wind is blowing towards west with 15 m/s and there is no ice – how large is then \(\tau_x\) and \(\tau_y\)? (See exercise 2)
4. In what direction (and with what speed) is the water in the surface (z=0) flowing? At the Ekman depth(z=-d)? At what depth is the current flowing in the opposite direction to the wind?
5. Try to plot the current! Why do you think we talk about an Ekman spiral?
6. When we send down our LADCP*** we get current profiles with a resolution of 8m (i.e we get one measurements for the current every 8 m) Do you think we are able to observe the Ekman spiral? Why/why not?

*** the LADCP is an instrument that we send down together with the CTD all the way to the bottom and that measures the current in the water on its way down (and up) so that we get profiles of current in addition to profiles of temperature and salinity.

Exercise 5

If you sum up (integrate) the current set up by the wind in the Ekman layer we get the transport, that is how much water that is moved in what direction due to the wind. We often call that the Ekman transport \(\vec{Q_{Ekman}}=U\vec{i}+V\vec{j}\), where

The unit of U and V is \(m^3/m/s\) (or \(m^2/s\)) and they give the amount of water that is flowing by per meter per second. The expression for \(\tau\) is given in exercise 2.

1. If it is blowing 15 m/s to the northeast and there is no ice, how larger is then U and V? In what direction is the water transported?
2. How large is the angle between the wind and the transport?
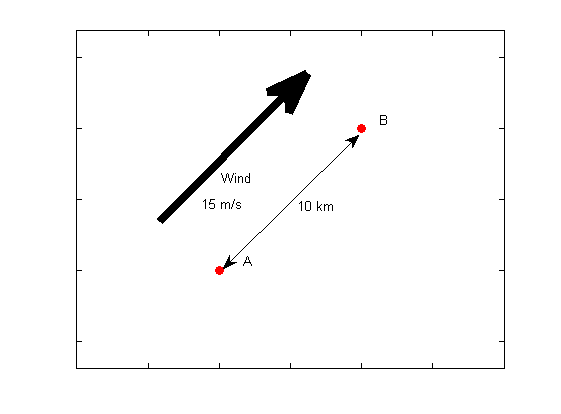
3. We have two buoys (see figure below) that are place 10 km apart and where a line between the buoys are parallel to the wind. How much water flows between the buoys per second? What do you think would have happened I the line between A and B would have been the coast?
4. In what direction do you think the water is blowing when the Bryggen in Bergen is flooded (the tides are also important, off cpurse!)
5. Along the coast of the Antarctic continent the wind is normally blowing towards the west – further north (60S) the wind is blowing to the east. Make a sketch showing the direction of the wind and the Ekman currents. What do you think happens in the middle? Discuss with your friends before reading the answer at the bottom of the page.

Convergence and divergence in the ocean

When the wind and thus the Ekman transport changes direction (or magnitude) from one region to another we get “convergence” or divergence. When we have divergence the surface water in an area “disappears” (i.e. it moves away and is not replenished) and new surface water must be provided from below. The water from depth is sucked up to the surface by the wind. In areas where this happens continuously (e.g. around Antarctica) we find large biological activity, since the water from depth is rich in nutrients. If you want to read more, then google e.g. “Wind driven upwelling”.

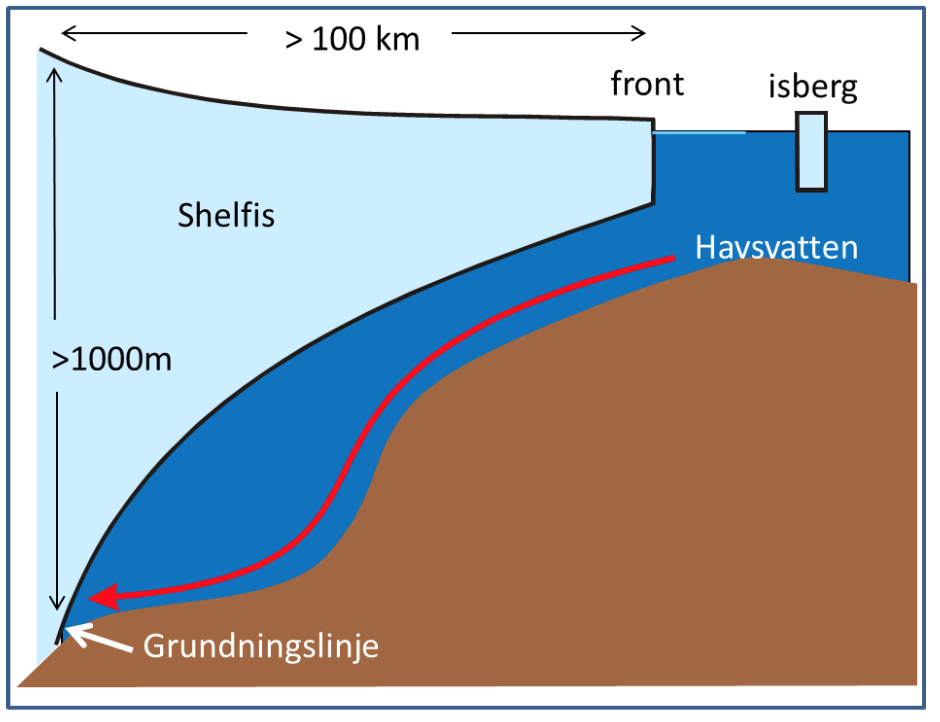
The freezingpoint of seawater sinks with increasing salinity and with increasing pressure – the more sline the water is, or the higher the pressure is, the more you can cool down the water before it freezes. Water from the tap freezes at 0 0\(^\circ\)C and sea water at -1.9\(^\circ\)C. At 1000m depth you can cool down seawater to -2.6\(^\circ\)C before it freezes. Below the large ice shelves around Antarctica seawater gets in contact with ice at large depths. When water is in contact with ice, it will melt ice and cool down to its freezing point. Below the Filchner-Ronne ice shelf in the Weddell Sea the grounding zone (see figure) is located at 1800 m depth. Here the water can become very cold!

Exercise 1

The freezing point is a function of salinity and pressure \(T_f=T_f(S,P)\). For a constant P (i.e. at one depth level) and for small changes in salinity the freezing point is a linear function of salinity and we can write \(T_f=kS+m\).

a) We know that \(T_f(S=34.4,P=0)=-1.8879^\circ C\) and \(T_f(S=34.7,P=0)=-1.9051^\circ C\). Determine the coefficients \(k\) and \(m\).

b) What is \(T_f(S=34.5,P=0)\)?

c) Vad är \(T_f(S=0,P=0)\)? Is this right? Why/why not??

In a similar manner, we have that (for a given salinity) \(T_f=kP+m\).

d) We know that \(T_f(S=34.5,P=0)=-1.8936^\circ C\) and \(T_f(S=34.5,P=1000dbar)=-2.6466^\circ C\). The pressure increase by about 1 dbar per meter, so the pressure is about 100 dbar at 100 m depth, 200 dbar at 200 m depth and son on. Determine the constants \(k\) och \(m\).

e) What is the freezing point at 2000 m depth?

f) My collegue Svein Østerhus have been drilling through the thick ice on the Filchner-Ronne ice shelf and made observations of the water in the cavity beneath the ice. The lowest temperature they observed was -2.53\(^\circ\)C, the salinity was 34.5. What is the smallest depth the observations can be from?

h) What temperatures could you expect to observe at the grounding line (1800m)

Exercise 2

When ice melts in salt water two things happen: the temperature sinks, since the heat from the water is used to melt the ice, and the salinity decreases, since the seawater is mixed with the fresh melt water. To melt a certain quantity of ice we need a certain quantity of heat, if we were to melt twice as much ice, we’d need twice as much heat. The change in temperature is proportional with the change in salinity \(k=\Delta T/\Delta S\)=2.4. A line with a slope of 2.4 in a TS-diagram (a diagram with salinity on the x-axis and temperature on the y-axis) shows how the the salinity and temperature changes when ice is melting in seawater. It is called a “Gade line” (see figure below) after professor H. Gade at UiB.

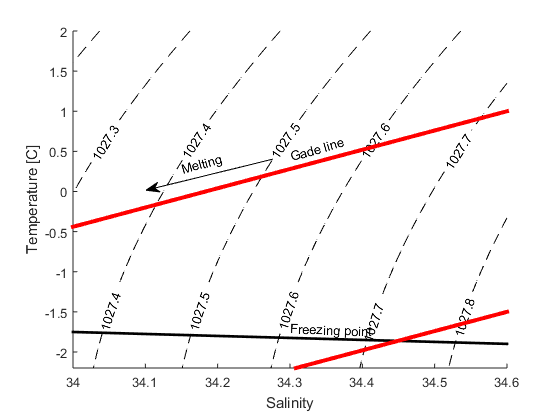
b) How salty is the water when T=0\(^\circ\)C?

c) How saline is the water when it is at its freezingpoint? Here you’ll need to use the expressin for the freezingpoint that you found in exercise 1 (P=0)

d) The figure below shows a TS-diagram with data from a CTD station  (ENG_Filchner_CTD)  that was occupied at the front of the Filchner ice shelf when I was there a few years ago. What was the lowest temperature we observed? How saline was that water?

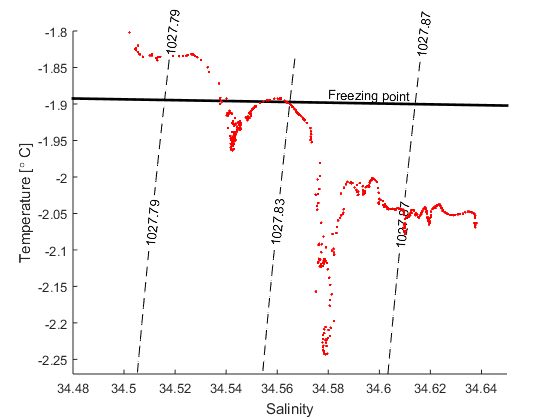
e) Find the expression for the Gade line that goes through the T,S point from (d) and plot it together with the data and the line that gives the freezing point (from exercise 1, P=0)

f) Most of the water entering the Filchner cavity is at its surface (P=0) freezing point. How saline was the coldest water thtat we observed when it entered the cavity, that is, before it melted ice?

Using the Gade line we can determine how saline the water that exit the cavity was when it entered the cavity. Since we know how the salinity changes along the front of the ice shelf (it increases the further west you go) we can also determine where the water entered the cavity

We go on scientific expeditions to the Amundsen Sea every other year or so, and then we do a lot of measurements and learn what things are like right then, when we are there. But we’d off course want to know also what happens when we are not around. To do so we deploy “moorings”. A mooring is and anchor, a line on which we attach instruments and floating elements to keep it upright in the water. The moorings are standing on the bottom and measures (normally currents, salinity and temperature but I’ll also have sensors to measure the concentration of oxygen) until we return a year or two later. What the mooring looks like and what instrument we put on it will depend on what we want to measure. At the bottom of the page there is a drawing of one of my moorings!

Exercise 1

Now you can design you mooring! What would it look like if you’d want to:

a) Study the evolution (salinity and temperature) of the surface layer (let’s say the upper 200 m) over a year in a area where the water is 500 m deep?

b) Study a bottom current that extends 300 m above the bottom

c) Find out how much warm water is entering the cavity below an ice shelf. The depth is 800 m and the draft of the ice shelf is 300 m deep (which means that ice bergs can reach just as deep!!)

Exercise 2

Do the following calculations for you mooring from above or for a mooring which has

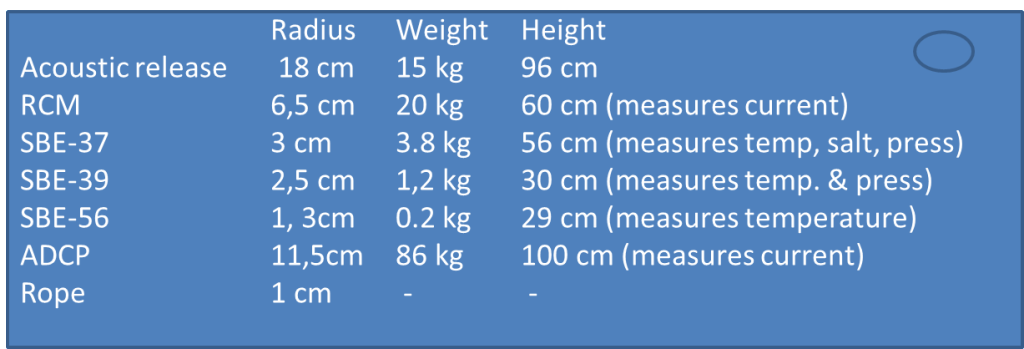
1 x acoustic release (25 mab); 3 X SBE37 (25, 150 and 300 mab), 1 x RCM (50 mab) 1 x ADCP (300 mab) and 5 x SBE56 (50, 75, 100, 200, 250 mab). Mab = meters above bottom.

The instrument has the following dimensions (they are all roughly equal to cylinders)

a) What is the weight of all the instruments in air? In water?

The mooring also needs floating elements to stand up in the water.

b) How much can one glass sphere lift? Their diameter is 43 cm and the weigh 22 kg in air.

c) How many spheres do we need to keep the mooring up right?

Exercise 3

When the current is strong it will tend to pull the mooring down towards the bottom – that is not good. Firstly, you don’t get measurements from the depth you wanted and secondly, many of the instrument cannot measure when they tilt too much, An ADCP, for example, cannot measure correctly if the tilt is above 15 \(^\circ\). So we need to add extra floating elements to make sure that the mooring is not pulled down if the current is strong. The force from the water pulling the mooring down is proportional to the area that the water hits (i.e. the cross sectional area of the mooring).

a) What percentage of the mooring cross sectional area is made up by the rope?

b) By how much is the area reduced if we change for a line that is 6 mm in diameter?

c) An instrument was pulled down to 170 mab and 218 m downstream, another instrument was pulled down to 65 mab and 105 m downstream. The shape of the line can be decribed by (half) a parable. Find the expression for the parable!

d) The pressure sensor on the ADCP shows that it now is 40 mab. How much is it tilting? Can we use the measurements?

e) How high up must it be (at least) for the measurements to be good?

f) Why do you think we prefer to have the ADCP high up looking down, rather than deep down looking up?

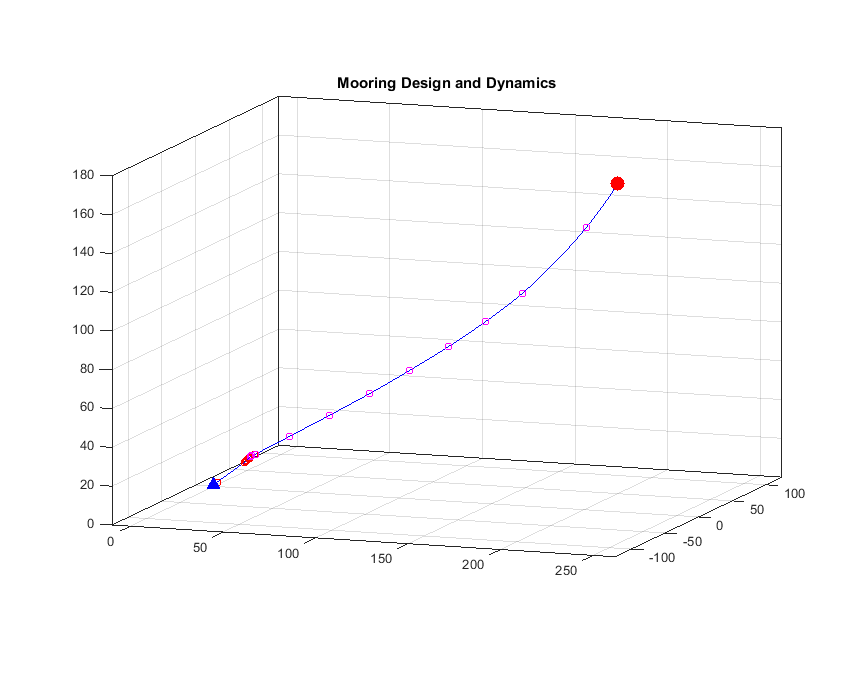
Exercise 4

When we retrieve the mooring and download the data from the instruments we get time series of current, temperature and salinity. We will now do some calciulations based on data from a mooring that was deployed in the Amundsen Sea in 2012.

a) Import and plot the current measurements from mooring S4, 17-24 June 2012 (ENG_Riggdata_S4_1). Describe what you see!

b) What is the mean current? In what direction was the water flowing? (\(u\) is the current in the \(x\)-direction (towards the east) and \(v\) is the current in the \(y\)-direction (towards the north))

c) If you were to describe the observations with a mathematical function, which one would you chose?

d) Determine the coefficient of your function!

e) An iceberg is floating with the current in the vicinity of S4. Set up an expression for it movement (using vectors) and plot its trajectory. How would you describe its movement?

f) Plot the current a week forward in time using your function from (d).

g) Import the data from S4 24/6-1/7 and plot it in the same figure. Is your model doing a good job predicting the currents? Why? Why not? (The file is named ENG_Riggdata_S4_2)

Exercise 5

Import and plot the measurements of pressure from mooring C2. The file is named ENG_Riggdata_C2. In this location the currents were much stronger than we expected and we had put on too little flotation 🙁

a) How would you interpret the record? (hint – look at exercise 2 above)

b) At what depth is the instrument located when the current is weak? (1 m \(\approx\) 1 dbar)

c) How deep is it pulled down?

d) What percentage of time is it pulled down more than 40 m? 80 m?

e) \(u\) gives the current in the \(x\)-direction (towards the east) and \(v\) gives the current in the \(y\)-direction (towards the north). Set up an expression for the current strength the calculate and plot it! How strong is the strongest current? The mean current? How many km/h is that?

f) Is there a relation between current strength and pressure (that is, the instrument pull- down?) Describe the relation mathematically and with words.

Exercise 6

The instruments are powered by batteries, and every time we make measurements we use a small amount – or a lot if it is an ADCP – energy. We want the instruments to keep measuring until we get back to pick them up – so we have to calculate beforehand how often we can make measurements without emptying the battery. But we also have to think about e.g. tides when determining how often to sample.

a) One of the components of the daily tides has a period of 25.8 h. The tidal current can be described by a sinus curve. The amplitude (and the phase) depends on where we are, but let’s assume the amplitude is 10 cm/s and the phase is 0. Set up an expression for the tidal current and plot it for 30 days.

b) If we made measurements only once a day, what would or time series look like?

c) What is the period of the “oscillation” that we would then observe?

d) The tidal current tha we observe is the sum of many components with different periods, amplitudes and phases. Another component has a period of 23.93h. Set up an expression for that tidal component if the amplitude is 9 cm/s. (You can set the phase to 0) and plot the sum of the two components. What do you see? How is the amplitude changing? How far is it between to “amplitude maximum”? Can you explain what you see? (hint: plot the components as well as the sum of them). Compare the results with the results from exercise 3!