February 2016 – Page 2 – Elin Darelius & Team

Uppgifter: Raka linjer och smältande is

Posted on 08/02/201619/01/2021 by Elin Darelius

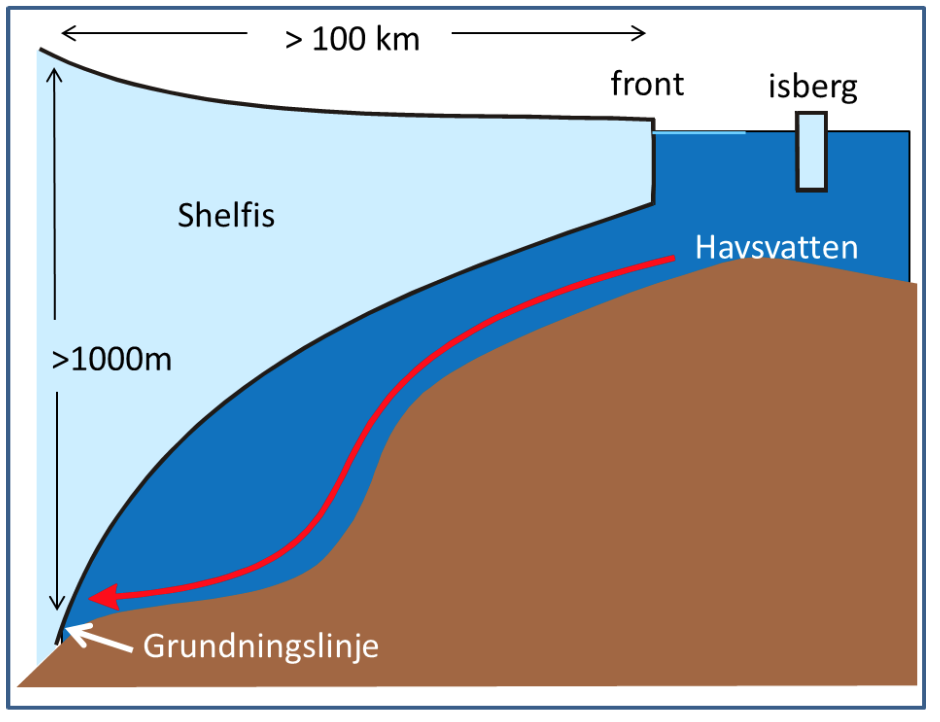
iskanten_antarktis — Så här ser en shelfis ut från sidan! Den röda pilen visar varmt vatten som strömmar in under isen

Fryspunkten till havsvatten sjunker med ökande salthalt och med ökande tryck – ju saltare vattnet är, eller ju högre trycket är ju mer kan man kyla det ner innan det fryser. Kranvatten fryser vid 0\(^\circ\)C – havsvatten vid -1.9\(^\circ\)C. På 1000 m djup kan man kyla ner vattnet till -2.6\(^\circ\)C innan det fryser. Under de stora shelfiserna i Antarktis kommer havsvatten i kontakt med is på stort djup. När vatten är i kontakt med is, så kommer det smälta is och kylas ner till fryspunkten. Under Filchner-Ronne shelfisen når vattnet ner vid grundningslinjen (se figur) till 1800 m djup . Då kan vattnet bli väldigt kallt!

Uppgift 1

Fryspunkten är en funktion av salthalt och tryck, \(T_f=T_f(S,P)\). För ett konstant P (dvs. på ett visst djup) och för små ändringar i S ändrar sig fryspunkten linjärt med salthalten och vi kan skriva \(T_f=kS+m\).

a) Vi vet att \(T_f(S=34.4,P=0)=-1.8879^\circ C\) och \(T_f(S=34.7,P=0)=-1.9051^\circ C\). Bestäm konstanterna \(k\) och \(m\).

b) Vad är \(T_f(S=34.5,P=0)\)?

c) Vad är \(T_f(S=0,P=0)\)? Stämmer det? Varför/varför inte?

På samma sätt kan vi, för en given salthalt, skriva \(T_f=kP+m\).

d) Vi vet att \(T_f(S=34.5,P=0)=-1.8936^\circ C\) och \(T_f(S=34.5,P=1000dbar)=-2.6466^\circ C\). Trycket ökar med ungefär 1 dbar per meter, så trycket är ca 100dbar på 100 m djup, 200dbar på 200 m djup och så vidare. Bestäm konstanterna \(k\) och \(m\).

e) Vad är fryspunkten när P=2000dbar (ca 2000 m djup)?

f) Min kollega Svein Østerhus har varit med och borrat genom den tjocka isen på Filchner-Ronne shelfisen i Weddell havet och gjort mätningar i havsvattnet i håligheten under isen. Den lägsta temperatur de mätte var -2.53\(^\circ\)C, salthalten var 34.5. Hur djupt måste de (minst) ha varit?

g) Hur kallt kunde vattnet ha blivit om det nått ner till grundningslinjen (1800 m) och smält is där?

Uppgift 2

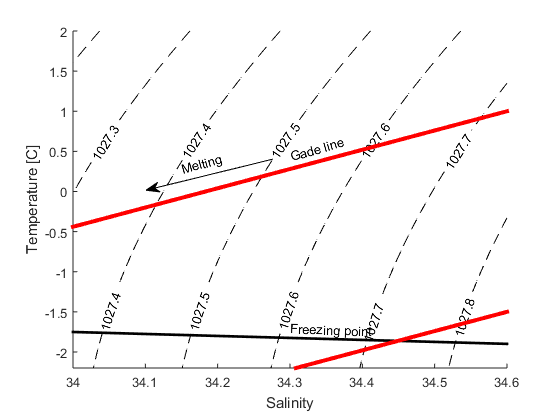
När is smälter i saltvatten så sker två saker: temperaturen sjunker, eftersom värmen från vattnet används till att smälta isen, och salthalten sjunker, eftersom saltvattnet blandar sig med smältvattnet från isen. För att smälta en viss mängd is behöver vi en viss mängd värme – ska vi smälta dubbelt så mycket is så behöver vi dubbelt så mycket värme. Förändringen i temperatur är \textit{proportional} med förändringen i salthalt: \(k=\Delta T/\Delta S\)=2.4. En linje med lutningen 2.4 i ett TS-diagram (ett diagram med salt på x-axeln och temperatur på y-axeln) visar hur salthalt och temperatur förändras när is smälter i havsvatten – den kallas för Gade-linje (se figur) efter Professor Herman Gade från UiB.

gade — TS-diagram som visar två Gade linjer (röda linjer) och fryspunkten (svart linje). I uppgifterna ska vi bestämma linjernas ekvationer och finna skjärningspunkt! De streckade linjerna visar isopyknaler. Iso betyder lik, pykno betyder densitet – så alla vattenmassor (punkter) på linjen har samma densitet. Siffrorna anger densiteten i kg/m3.

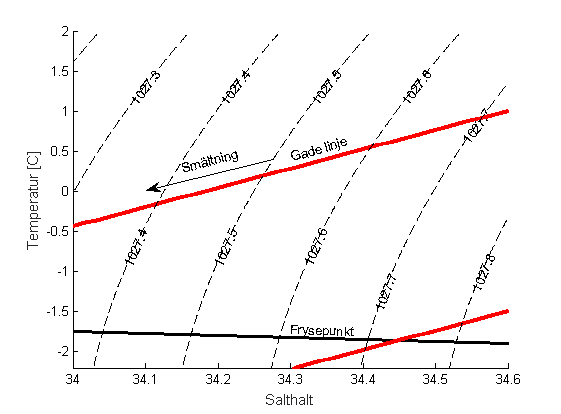
a) Finn ekvationen (\(T=kS+m\)) som beskriver hur temperaturen förändrar sig när is smälter i vatten som har T=2\(^\circ\)C och S=34.6? Plotta den i et TS-diagram (En graf med salthalt på \(x\)-axeln och temperatur på \(y\)-axeln).

b) Hur salt är vattnet när T=0\(^\circ\)C?

c) Hur salt är vattnet när vattnet är på fryspunkten? Här behöver du använda uttrycket for fryspunkten som du kom fram till i uppgift 1 (P=0).

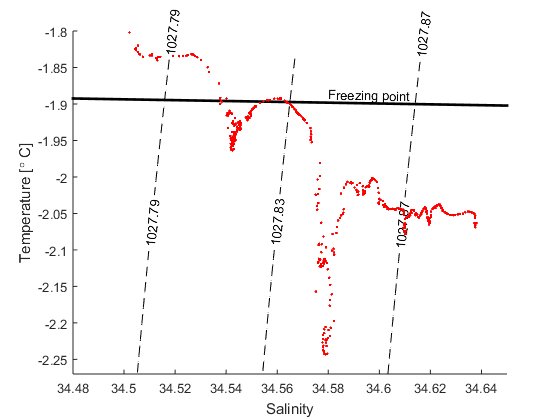
d) Figuren nedan visar ett TS-diagram med data från en CTD station som togs vid vid fronten av Filchner shelfisen när jag var där för några år sen. Vad var den lägsta temperaturen som vi mätte då? hur salt var det vattnet? Hur kan det ha blivit så kallt?

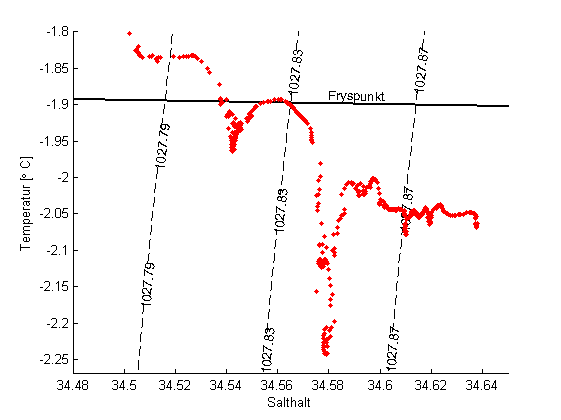
TS-diagram som visar data från en station vid fronten av Filchner shelfisen. Den svarta linjen visar fryspunkten (för P=0).

e) Finn Gade linjen som går genom punkten med det kallaste vattnet vi observerade och plotta den tillsammans med datan och linjen som ger frysepunkten (från uppgift 1, P=0) .

f) Det mesta av vattnet som kommer in under Filchner-Ronne isen är på fryspunkten (P=0). Hur salt var det kallaste vattnet som vi observerade när det kom in under shelfisen, dvs innan det smälte is?

Med hjälp av Gade linjen kan vi bestämma hur salt vattnet som kommer ut från håligheten under Filchner-Ronne shelfisen var när det strömmade in. Eftersom vi vet hur salthalten ändrar sig längst fronten (det blir saltare ju längre väst man går) så kan vi också säga var det vattnet strömmade in!

Exercise: Straight lines and melting ice

Posted on 08/02/201619/01/2021 by Elin Darelius

An ice shelf from the side! The red arrow shows warm water entering the ice shelf cavity.

The freezingpoint of seawater sinks with increasing salinity and with increasing pressure – the more sline the water is, or the higher the pressure is, the more you can cool down the water before it freezes. Water from the tap freezes at 0 0\(^\circ\)C and sea water at -1.9\(^\circ\)C. At 1000m depth you can cool down seawater to -2.6\(^\circ\)C before it freezes. Below the large ice shelves around Antarctica seawater gets in contact with ice at large depths. When water is in contact with ice, it will melt ice and cool down to its freezing point. Below the Filchner-Ronne ice shelf in the Weddell Sea the grounding zone (see figure) is located at 1800 m depth. Here the water can become very cold!

Exercise 1

The freezing point is a function of salinity and pressure \(T_f=T_f(S,P)\). For a constant P (i.e. at one depth level) and for small changes in salinity the freezing point is a linear function of salinity and we can write \(T_f=kS+m\).

a) We know that \(T_f(S=34.4,P=0)=-1.8879^\circ C\) and \(T_f(S=34.7,P=0)=-1.9051^\circ C\). Determine the coefficients \(k\) and \(m\).

b) What is \(T_f(S=34.5,P=0)\)?

c) Vad är \(T_f(S=0,P=0)\)? Is this right? Why/why not??

In a similar manner, we have that (for a given salinity) \(T_f=kP+m\).

d) We know that \(T_f(S=34.5,P=0)=-1.8936^\circ C\) and \(T_f(S=34.5,P=1000dbar)=-2.6466^\circ C\). The pressure increase by about 1 dbar per meter, so the pressure is about 100 dbar at 100 m depth, 200 dbar at 200 m depth and son on. Determine the constants \(k\) och \(m\).

e) What is the freezing point at 2000 m depth?

f) My collegue Svein Østerhus have been drilling through the thick ice on the Filchner-Ronne ice shelf and made observations of the water in the cavity beneath the ice. The lowest temperature they observed was -2.53\(^\circ\)C, the salinity was 34.5. What is the smallest depth the observations can be from?

h) What temperatures could you expect to observe at the grounding line (1800m)

Exercise 2

When ice melts in salt water two things happen: the temperature sinks, since the heat from the water is used to melt the ice, and the salinity decreases, since the seawater is mixed with the fresh melt water. To melt a certain quantity of ice we need a certain quantity of heat, if we were to melt twice as much ice, we’d need twice as much heat. The change in temperature is proportional with the change in salinity \(k=\Delta T/\Delta S\)=2.4. A line with a slope of 2.4 in a TS-diagram (a diagram with salinity on the x-axis and temperature on the y-axis) shows how the the salinity and temperature changes when ice is melting in seawater. It is called a “Gade line” (see figure below) after professor H. Gade at UiB.

TS-diagram showing two Gade lines (red lines) and the freezing point (black line). In the exercises we will determine the equations of the lines to find were they cross each other. The dashed lines are isopycnals. Iso means equal, pykno means density - so all water masses (points) on the line has the same density). The number gives the density in kg/m\(^3\). — TS-diagram showing two Gade lines (red lines) and the freezing point (black line). In the exercises we will determine the equations of the lines to find were they cross each other. The dashed lines are isopycnals. Iso means equal, pykno means density – so all water masses (points) on the line has the same density). The number gives the density in kg/m[latex]^3[/latex].

a) Find the equation (\(T=kS+m\)) that describes how the temeprature and salinity changes when ice is melting in water with T=2\(^\circ\)C and S=34.6? Plot the line in a TS-diagram.

b) How salty is the water when T=0\(^\circ\)C?

c) How saline is the water when it is at its freezingpoint? Here you’ll need to use the expressin for the freezingpoint that you found in exercise 1 (P=0)

d) The figure below shows a TS-diagram with data from a CTD station (ENG_Filchner_CTD) that was occupied at the front of the Filchner ice shelf when I was there a few years ago. What was the lowest temperature we observed? How saline was that water?

TS-diagram showing data from a station at the front of the Filchner ice shelf. The black point show the freezing point (P=0).

e) Find the expression for the Gade line that goes through the T,S point from (d) and plot it together with the data and the line that gives the freezing point (from exercise 1, P=0)

f) Most of the water entering the Filchner cavity is at its surface (P=0) freezing point. How saline was the coldest water thtat we observed when it entered the cavity, that is, before it melted ice?

Using the Gade line we can determine how saline the water that exit the cavity was when it entered the cavity. Since we know how the salinity changes along the front of the ice shelf (it increases the further west you go) we can also determine where the water entered the cavity

Eksperiment: Hvor kaldt kan vannet bli?

Posted on 08/02/201619/01/2021 by Elin Darelius

Du trenger:

En skål
Et termometer
Isbiter
Salt
Litt vann
Noe å røre med

Bland vann og isbiter i en skål og sett i termometeret. Rør godt om en stund. Hva viser termometeret?

Hell oppi salt og rør godt om. Hva skjer med termometeret? Hva skjer om du heller oppi enda mer salt? Hvor kaldt kan du få vannet?

Når en blanding av vann og is er i likevekt, så er temperaturen på frysepunktet. Når du heller i salt senkes frysepunktet (jo saltere vannet er, jo lavere er frysepunktet) og blandingen er ikke lenger i likevekt. Varme fra vannet brukes til å smelte is og temperaturen synker, enten til alt isen er smeltet eller til temperaturen i vannet er på frysepunktet.

Experiment: Hur kallt kan vattnet bli?

Posted on 08/02/201619/01/2021 by Elin Darelius

Du behöver:

En skål
En termometer
isbitar
lite vatten
något att röra med

Blanda vatten och isbitar i en skål och sätt i termometern. Rör om ordentligt en stund. Vad visar termometern?

Slå så i salt och rör om ordentligt. Vad händer med termometern? Vad sker om du slår i ännu mer salt? Hur kallt kan du få vattnet?

När en blandning av vatten och is är i jämvikt, så är temperaturen på fryspunkten. När du slår i salt, så sänks fryspunkten (ju saltare vattnet är, ju lägre är frysåunkten) och blandningen är inte längre i jämvikt. Värme från vattnet används till att smälta is och temperaturen sjunker – antingen tills all isen är smält, eller tills temperaturen i vattnet är på frysepunkten.

Experiment: How cold can water get?

Posted on 08/02/201619/01/2021 by Elin Darelius

You need:

a bowl
a thermometer
ice cubes
salt
some water
something to stir with

Add water and ice cubes to the bowl and then add the thermometer. Stir a bit. What does the thermometer show?

Now add a little salt and stir well to solve the salt in the ice water. What happens to the temperature? What happens if you add even more salt? How cold can you get your water?

When a mixture of water and ice is in equilibrium, the temperature is at freezing point. When you add more salt, that lowers the freezing temperature (the more salt, the lower the freezing point) and the mixture is no longer in equilibrium.

Heat from the water is used to melt, and the temperature of the mixture sinks, either until all ice as melted, or until the temperature of the water is the freezing temperature.

Alla mina riggar i vattnet

Posted on 04/02/201619/01/2021 by Elin Darelius

Den här veckan kommer det blog från min kollega Svein Østerhus som befinner sig på en annan forskningsbåt, på andra sidan av kontinenten men jag tänkte ändå att ni skulle få en kort uppdatering (och ett nytt problem) från mig!

6861600114_bb8d69230f_o — Foto: Povl Abrahamsen

Alla mina riggar är nu i vattnet – och det är en betydligt mindre nervös Elin som går och lägger sig om kvällen nu än det var tidigare. Det är mycket som ska förberedas, mycket man ska tänka på när man sätter ihop riggarna, så många bitar som ska passa ihop – och mycket som kan gå fel. Vanligvis har jag en tekniker med mig som har full koll på vilka muttrar som ska sitta var och i vilken ordning ringar och shacklar ska sitta, men nu var det jag som stod där ute på däck med skiftnyckeln i handen och skulle hålla ordning på allting – och se till att allting var färdigt när det var min tur. Men det gick bra! Och så var Araon till slut på rätt position och vi kunde börja!

Mr Ham, den koreanska riggteknikern, ger tecken till kranföraren och snart ligger min första oranga boj och guppar i vattnet bakom båten. Vi kör långsamt framåt och matar ut lina från vinshen allteftersom – var femtionde meter fäster jag och Karen instrumenter på linan. Det går fort, alla vet vad de ska göra. Bojen blir mindre och mindre och snart är 300 m med lina utvinschad och alla instrumenter är i vattnet. Det är bara ankaret (3 gamla
järnvägshjul) som står kvar på akterdäck – men snart försvinner också det ner i djupet med ett stort plask. Den stora oranga bojarna dras fram genomvattnet mot oss allteftersom ankaret sjunker, men tillslut fösvinner också de under ytan. Ankaret kommer till slut att landa på botten – vanligtvis någonstans mittemellan platsen där det blev släppt ner och platsen där den sista bojen
försvann under ytan – men för att vi ska veta exakt* var riggen står så “triangulerar” vi med hjälp av utlösaren. På tre olika platser skickar vi ner signaler till utlösaren och ber honom svara -och utifrån tiden det tar för svaret att komma tillbaka kan vi räkna ut avståndet mellan båten och utlösaren. Eftersom vi vet var båten är, så kan vi räkna ut var riggen står… kanske ni vill hjälpa till? Jag tror det är enklast att lösa problemet grafiskt!

När vi släppt ner ankaret till min första rigg så åkte vi först 443 m i riktning -40.2 grader (se förklaring längst ner) till första trianguleringspunkten. Då var avståndet till utlösaren 802m. Därifrån åkte vi 862 m i riktning 172 grader och fick ett avstånd på 754 m. På den sista punkten var avståndet till utlösaren 816 m. Då hade vi åkt vi 867 m i riktning 53.0 grader från punkt nummer 2. Det är 600 m djupt och utlösaren sitter 25 m över botten. Hydrofonen som vi använder för att prata med utlösaren sänker vi ner 10 m under ytan. Var står riggen? Hur långt hade ankaret drivit? Hur noggrann är trianguleringen? Kan du uppskatta felet?

Däcksenheten som pratar med utlösaren använder en ljudhastighet på 1497 m/s när den beräknar avståndet till utlösaren. Med hjälp av data från en CTD-profil så beräknade jag den faktiska ljudhastigheten (som är en function av salthalt, temperatur och tryck) och kom fram till att medelhastigheten bara var 1447 m/s. Spelar det någon roll i uträkningarna ovan? Kan du korrigera dina beräkningar? Riktningarna angivs som “grader motsols från x-axeln”. X-axeln pekar mot öst, så om vi åker mot öst så är vinkeln noll grader, om vi åker mot norr så är vinkeln 90 grader och om vi åker söderut så är vinkeln -90 grader.

Oppgaver og øvelser

Norsk

Svenska

All the moorings in the water!

Posted on 04/02/201619/01/2021 by Elin Darelius

This week you’ll get a letter from my colleague Svein Osterhus who is onboard another research ship on the other side of the continent… but I thought I’d send you a short update from the Amundsen Sea and a new problem for you to solve!

All of my moorings are now in the water – and the nervous butterflies that have flown around in my belly the last couple of weeks are finally gone! There are so many things to prepare, so many things to think about when putting the moorings together – so many things that can go wrong. When I’ve deployed moorings before I’ve always had a technician with me, a technician who has full control over what screw goes where and where those shackles and rings are supposed to be… but this time it was me who was out on deck with a spanner in my hand trying to get everything ready in time. Finally Araon got into position and we could start!

Mr Ham, the Korean mooring technician, gave sign to the winch driver and he elegantly lifts my first orange buoy into the water. Araon is slowly advancing as we feed the mooring line out behind us. Every fifty meter or so mr Ham stops, and Karen and I attach an instrument to the line. Everything goes quick and smoothly – we all know what to do. The buoy gets smaller and smaller in the distance, and soon there is 375 m of mooring line out in the water. Only the anchor (3 old railway wheels) is left on deck, and finally it too disappears into the water with a splash. The orange buoys are pulled through the water as the anchors sinks, but eventually gravity wins and they too are gone. The anchors sinks down and lands on the bottom, normally somewhere between the location it was released and the place where the buoys are last seen. To find out exactly where the mooring is, we use the acoustic release to “triangulate”. At three positions we send down signals to the acoustic release, and based on the time it takes from the signal to come back we can calculate the distance between the hydrophone that we lower into the water to talk to the acoustic releaser and the releaser itself. Since we know where the boat is, we can determine where the releaser (and thus the mooring) is located… maybe you’d want to help out?

When the anchor to the first of my moorings were released we moved 443 m towards -40.2 degrees (see explanation of the directions in the end) and the first triangulation point. The distance to the releaser was then 802 m. Thereafter we moved 862 m towards 172 degrees and got a distance of 754 m. At the last point, the distance to the releaser was 754 m. Then we’d moved 867 m in towards 53 degrees from point number two. The depth is 600 m and the releaser is locate 25 m above the anchor. The hydrophone was lowered 10 m into the water.

Where is the anchor? How far had the anchor drifted? How exact is the triangulation? Can you estimate the error?

The deck unit talking to the acoustic release assumes a sound speed of 1497 m/s when calculating the distances. Using data from our CTD cast we calculated the true sound speed (which is a function of salinity, temperature and pressure) and found the mean speed of sound to be 1447 m/s. Does that matter for the calculations above? Can you correct for it?

The directions are given as degrees counterclockwise from the x-axis. The X-axis is pointing eastward, so if we go towards the east, the direction is 0 degrees, if we go north, it is 90 degrees and if we go south, it is -90 degrees.

Do the Math! Straight lines and melting ice

Experiment: How cold can water get?

Riggar på väg upp – och riggar på väg ned

Posted on 01/02/201619/01/2021 by Elin Darelius

Med CTD och LADCP (strömmätare som sitter på CTD:n) får vi reda på hur vattnet strömmar och vilken temperatur det har just nu, när vi är här – men vi vill så klart också veta vad som händer när vi rest hem igen. Därför sätter vi ut instrumenter på så kallade riggar som kan stå kvar och mäta när vi åkt hem, och så kan vi komma tillbaka och hämta dem senare. Jag har aldrig varit i Amundsenhavet tidigare, så jag har inga riggar att plocka upp jag ska bara sätta ut nya. Mina svenska, engelska och Koreanska kollegor har riggar i vattnet – och det var med stor spänning vi tidigare i veckan närmade oss platsen där en av dem för två år sen sattes ut. Karen skickade hydrofonen över relingen och ner i vattnet och knappade in utlösarens speciella kod. Långt under oss nere på botten stod den och väntade snällt på att få höra från oss – och när den efter två år nu äntligen gjorde det så svarar den glatt “jag är här!”. Karen knappade in en ny kod som betyder “släpp”, och snart fick hon ett nytt svar “jag har släppt, jag är på väg upp!”. Alla spejade ut i dimman – ivriga att vara den första som fick syn på de gula bojarna.
– Där är den! Där borta!
Besättningen är snabbt ut i en mindre båt för att börja arbetet med att plocka upp riggen – de vet vad de ska göra, det här har de gjort förr. Några timmar senare är alla instrument ombord och vi arbetar för fullt. All data ska lastas över från instrumenten till datorer och hårddiskar, sedan ska instrumenten gås över och få nya batterier och programmeras. Imorgon ska de ner i vattnet igen!
Koreanerna hade inte lika tur; deras första rigg hade gått av en bit ovanför botten och det var bara utlösare och ett par temperatursensorer som kom upp. Deras andra rigg var helt borta – troligtvis är det ett stort isberg som dragit den med sig. Men de sista tre kom upp som på beställing!

Första riggen är redo att gå i vattnet – dags att säga “Hej då” till mina “mikrokatter”. Förhoppningsvis ses vi igen om två år! (Foto: Nicole Waite)

I går hade vi möte med besättning och tekniker för att gå igenom hur mina riggar ser ut och för att bestämma hur vi bäst sätter ut dem. Besättningen talar dålig eller ingen engelska*, så mötet hölls på koreanska – och bara då och då kom det en fråga på engelska till mig. I en knapp timme lät det ungefär så här:

ㄻㅊ널촘ㅈ괴ㅓㄴ모거모 ㅏㄱ mooring ㅓ로ㅕ추마 ADCP ㅕ루 멍로 ㅏㅕ고러ㅏㅓ Shackleㄷ ㅣ찰머놀ㄹ러ㅏmooring 몬염ㅍ뒤곤?mooring름 ㅡㅐㅐA-frame 갸ㅜㅎ 멀촘너 .

… och där försvinner utlösaren över relingen! (Foto: Nicole Waite)

Jag har i lugn och ro förberett mina instrumenter och min utrustning – i tron om att det fortfarande var flera dagar kvar tills de skulle i vattnet. Koreanerna hade fyra riggar kvar att sätta ut först. Men så blåste det upp och helt plöstligt gick vågorna höga – och kaptenen gav order om att det var för farligt att arbeta på däck… så nu har de vänt hela arbetsschemat på huvudet och vi kör med full fart västerut, till västra delen av Getz shelfis. Där är det mer is och förhoppningsvis mindre vågor, och desutom kan vi då använda tiden med dåligt väder till att förflytta oss, istället för att ligga och vänta på att vi ska kunna sätta ut riggar. Så nu är det helt plöstligt min sista rigg som står överst på dagordningen …och jag har tyvärr inte tid att skriva mer till er just nu!

*Jag frågade La, en av oceanograferna som pratar bra engelska var han lärt sig språket. De andra som pratar bra engelska har alla gjort doktorgrad eller bott utomlands – men jag visste att han inte har gjort det. Efter en stund kom det fram att han under studietiden en gång i veckan pratat engelska med de enda i Korea som är villiga att prata engelska med dig helt gratis: Jehovas vittnen och mormoner! “Men jag är fortfarande Buddhist, jag ville bara lära mig prata engelska och hade inte råd med privat lärare…”

Oppgaver og øvelser

Norsk

Svenska

Mooring on the way up – and mooring on the way down.

Posted on 01/02/201619/01/2021 by Elin Darelius

With a CTD and LADCP (current meters mounted on the CTD) we can understand where the water is flowing and what its temperature is right now that we are here – but we will also be able to see what happens when we are back home already. We deploy the instruments on so-called “moorings” that stay in the ocean and measure while we are gone, and that we will come and pick up next year or the year after. I have never been in the Amundsen Sea before, so I don’t have moorings to recover right now, only new ones to deploy. But my Swedish, English and Korean colleagues do have moorings in the water – and we are getting more and more excited as we are coming closer to the position where those moorings were deployed two years ago! Karen holds a hydrophone over the railing and down into the water. Then she keys in the releaser’s special code. Far away, deep beneath us on the sea floor, the mooring waits to hear from us – and finally, now, after two years in the ocean, it can reply “here I am!”. Karen types in a second code which means “let go!”, and right away she gets the reply from the mooring: “I’ve let go, I am on my way up!”. All of us are excitedly watching the sea – keen to be the first person to spot the yellow buoy.

– There it is! There it is!

The crew has deployed a small boat to go and fetch the mooring – they know exactly what to do, they have done it many times before.

A couple of hours later all instruments are on board and we are working hard. All data needs to be downloaded to our computers and stored to hard drives. Later, the instruments are turned over and get new batteries and software. Tomorrow they are going back into the sea!

The Koreans weren’t lucky this time round; their first mooring had broken off a bit above the sea floor and therefore they could only recover the releaser and a couple of thermometers. Their other mooring was completely gone – it was probably dragged away by a large iceberg. But the last three came up exactly as planned!

Yesterday we had a meeting with the crew and technicians to talk through what my mooring looks like and to decide how to best deploy it. The crew speaks little or no English*, therefore the meeting was held in Korean – only every now and then I was asked something in English. For almost an hour it sounded pretty much like this:

I took my time and carefully prepared my instruments and tools – trusting that it would be several days before my moorings should go out into the water. The Koreans had four moorings that should go out first. But it got really windy and the waves got higher and higher – and the captain gave the order to stop working on deck because it was too dangerous… And this messed up the whole work schedule! We steamed westward at full speed, to the western part of Getz ice shelf. There is more ice there, and hopefully less waves, so we can use the time while the weather is bad to steam there instead of just waiting around for the weather to get better until we can deploy our moorings. So now it is all of a sudden my last mooring that shall go out right now… and therefore, I unfortunately don’t have time to write more right now!

*I asked La, one of the oceanographers who speaks excellent English, how he learned the language. All the others who speak English well did their PhDs or studies aboard – but I knew La hadn’t done that. After a while I found out that during his studies, he once a week talked in English with those people in Korea who want to talk to you in English for free: Jehova’s witness and Mormons! “But I am still a Buddhist, I just wanted to learn English and couldn’t afford a private teacher…”

Do the Math! Moorings and time series

Experiments:

Archimedes principle

What floats in the dead sea?

Oppgaver: Rigger og tidsserier

Posted on 01/02/201619/01/2021 by Elin Darelius

Vi reiser på tokt til Amundsenhavet annenhvert år og gjør masse målinger. Slik får vi et bilde av hva som skjer i det tidsrommet vi er der. Men vi vil selvsagt også vite hva som foregår når vi ikke er der. Derfor setter vi ut «rigger». En rigg er kort sagt et anker, en line som vi fester instrumenter på, og deretter flyteelementer som holder den oppe. Riggen plasseres på bunnen og måler (vanligvis hastighet, salt og temperatur, men vi skal også ha instrumenter som måler konsentrasjonen av oksygen i vannet) til vi kommer tilbake ett eller to år senere og plukker den opp igjen. Hvordan riggen ser ut og hvilke instrumenter som settes på er avhengig av hva man skal studere. I tabellen i oppgave 2 finner du informasjon om noen av instrumentene vi bruker og her ser du hvordan en av mine rigger ser ut: rigg

Oppgave 1

Nå kan du få designe din egen rigg! Hvordan skulle den sett ut om du ville…

a) studere hvordan vannets saltholdighet og temperatur forandrer seg i de øvre 200 m i løpet av ett år i et område som er 500 m dypt?

b) studere en bunnstrøm som når opp til 300 m over bunn?

c) finne ut hvor mye varmt vann som strømmer inn under en isbrem? Det er 800 m dypt. Tenk på at isbremmen kan være 300 m dyp.

Oppgave 2

Gjør beregninger for din egen rigg eller for en rigg som har:

1 x utløser (25 mob); 3 x SBE37 (25, 150 og 300 mob), 1 x RCM (50 mob), 1 x ADCP (300 mob) og 5 x SBE56 (50, 75, 100, 200, 250 mob). Mob=meter over bunn.

Instrumentene har følgende dimensjoner (alle er omtrent sylinderformet):

a) Hvor mye veier instrumentene på riggen i luft? I vann?

Riggen må også ha flyteelementer (glasskuler) for å holde seg vertikal!

b) Hvor stor er oppdriften fra en glasskule? Glasskulenes diameter er 43 cm og har en masse på 22 kg.

c) Hvor mange glasskuler trenger vi for å holde riggen oppe?

Oppgave 3

Når det er sterk strøm så dras riggen ned mot bunn – det er ikke bra! For det første så får man ikke målinger fra det dypet man hadde tenkt, og for det andre så kan mange instrument ikke måle når de heller for mye. En ADCP kan for eksempel ikke måle strømmen om den heller mer enn 15\(^\circ\). Derfor setter vi på ekstra flyteelementer for å holde riggen vertikal også når det er sterk strøm. Kraften som det strømmende vannet utøver på riggen er proporsjonal med området (arealet) som vannet treffer.

a) Hvor stor andel av riggens areal utgjør linen?

b) Hvor mye minsker motstanden om vi bytter til en line som bare er 6 mm i diameter?

c) Et instrument har blitt dratt ned til 170 m over bunnen (mob) og dratt 218 meter nedstrøms. Et annet instrument har blitt dratt ned til 65 mob og 105 meter nedstrøms. Formen på linen kan beskrives med en (halv) parabel. Finn uttrykket for parabelen.

d) Trykksensoren på en ADCP viser at den nå sitter 40 mob. Hvor mye heller den da? Kan vi bruke målingene?

e) Hvor høyt opp måtte ADCP’en ha vært for at vi skulle kunne bruke målingene?

f) Hvorfor tror du vi heller setter en ADCP høyt oppe så den «ser» nedover enn en som sitter nær bunn og «ser» opp?

mooring2 — En av mine rigger i sterk strøm. Vi bruker dataprogram for å beregne hvordan riggene kommer til å oppføre seg i sterk strøm. Programmet forteller oss også hvor tungt ankeret må være.

Oppgave 4

Når vi henter opp riggen igjen og laster ned dataene fra instrumentene får vi tidsserier av strøm (hastighet), temperatur, og saltholdighet. Nå skal vi kikke på data fra rigger som stod ute i Amundsenhavet i 2012

a) Les inn og plot strømmålingene fra rigg S4 mellom 17-24 juni, 2012. (Riggdata_S4_1). Strømmålingene er i cm/s. Hva er det vi ser?

b) Hva er middelstrømmen? I hvilken retning går den? (\(u\) gir strømstyrken i \(x\)-retning (mot øst) og \(v\) gir strømmen i \(y\)– retning (mot nord)).

c) Om du skal tilpasse eller beskrive observasjonene med en funksjon , hvilken velger du da?

d) Bestem konstantene ved hjelp av regresjon.

e) Et isfjell flyter med strømmen i nærheten av S4 – sett opp et utrykk (på vektorform) for hvordan isfjellet kommer til å forflytte seg og plott trajektorien i en ny figur. Beskriv bevegelsen.

f) Plott strømmen en uke fram i tid ved hjelp av din funksjon fra (d).

g) Les inn data fra S4 24/6 – 1/7 og plott den i samme figur – stemmer det med din modell? Hvorfor/hvorfor ikke? (Filen heter: Riggdata_S4_2).

Oppgave 5

Les inn i plott trykkmålingene fra rigg C2. Her var strømmen mye sterkere enn vi trodde, og vi hadde ikke satt på tilstrekkelig med flyteelementer 🙁 (Filen heter: Riggdata_C2).

a) Hva er det vi ser? (hint: se oppgave 2)

b) Hvor dypt sitter instrumentet når det er svak strøm? (1 m \(\approx\) 1 dbar)

c) Hvor dypt dras det ned maksimalt?

d) Hvor stor del av tiden har det blitt dratt ned mer enn 40 m? 80 m?

e) \(u\) gir strømstyrken i \(x\)-retning (mot øst) og \(v\) gir strømmen i \(y\)– retning (mot nord). Bruk Pythagoras og sett opp et uttrykk for strømstyrken. Regn ut strømmen! Hvor sterk er den sterkeste strømmen? Middelstrømmen? Hvor mange kilometer per time er det?

f) Er det noen sammenheng mellom strømstyrke og trykk (dvs neddragning)? Hvordan ser det ut? Beskriv sammenhengen matematisk og forklar med ord.

Oppgave 6

Instrumentene går på batteri – og hver gang de gjør en måling brukes det litt (eller mye om det er en ADCP) energi. Vi vil selvsagt at instrumentene skal gjøre målinger helt til vi kommer tilbake og henter riggen, så vi regner ut på forhånd hvor ofte vi kan gjøre målinger uten at batteriet tar slutt. Men vi må også ta hensyn til for eksempel tidevann når vi bestemmer hvor ofte vi skal måle.

a) Det daglige tidevannet (en av komponentene) har en periode på 25.8 timer. Tidevannet kan beskrives med en sinus kurve. Amplituden (og fasen) avhenger av hvor vi er, men anta at amplituden er 10 cm/s og fasen er 0. Sett opp et uttrykk som beskriver tidevannet og plott det tretti dager fram i tiden.

b) Om vi hadde gjort målinger bare en gang om dagen (dvs hver 24 h), hvordan hadde vår tidsserie sett ut da?

c) Hvilken periode har «svingningen» som vi da observerer?

d) Tidevannet som vi observerer er en sum av mange tidevannskomponenter med ulike perioder. En annen heldaglig tidevannskomponent har en periode på 23,93 timer. Sett opp uttrykket for den tidevannskomponenten dersom amplituden er 9 cm/s (fasen kan du sette til null) og plott summen av de to komponetene. Hva ser du? Hvordan endres amplituden? Kan du forklare hva som skjer? (tips – plott både de ulike komponentene og summen av dem). Sammenlign resultatet med resultatene dine fra oppgave 3g.

Month: February 2016

Uppgift 1

Uppgift 2

Exercise 1

Exercise 2

Oppgaver og øvelser

Oppgaver og øvelser