
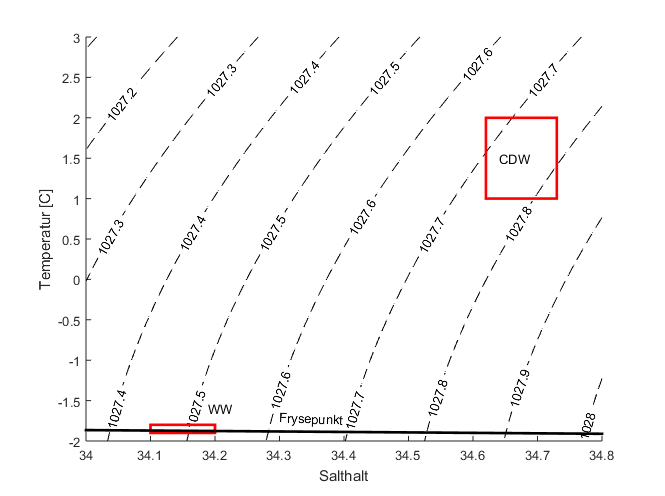
Vi oceanografer pratar ofta om “vattenmassor”, det är vatten med olikt ursprung och som därför har olik salthalt och temperatur. Vi pratar till exempel om Atlantiskt vatten som är varmt och salt, om Antarktiskt ytvatten som är kallt och färskt eller om Antarktiskt sockelvatten som är kallt och salt. Det är till stor del atmosfären som bestämmer vattenmassornas egenskaper. Där det är varmt värms vattnet upp, där det är kallt, kyls havet ned. Salthalten bestäms av avdunstning, färskvannstillförsel (från älvar och åar eller från regn eller snö) och utav isfrysning. När det bildas is om vintern, är det vattenmolekylerna som fryser. Det mesta av saltet blir skiljt ut, och salthalten i vattnet under ökar. I grunda områden där det bildas mycket is – till exempel inne på vissa av de Antarktiska kontinentalsocklarna – kan vattnet bli väldigt salt och därmed blir vattnet väldigt tungt. När isen sen smälter om våren, så bildas det ett färskt, lätt lag ovanpå det salta. I uppgiften härintill nämns “Circumpolar Deep Water”, CDW. CDW är egentligen en blanding av flera vattenmassor, däribland vatten som kommer helt från nordatlanten. CDW har en temperatur mellan 1 och 2 grader och en salthalt mellan 34.62 och 34.73. Salthalten har konsigt nog ingen enhet, men det motsvarar ungefär promille. Om salthalten är 1 så är det 1 gram salt per kilo vatten. Salthalten i havet är typiskt 35, eller ca 3.5 %.
I ett TS-diagram (en figur med salthalt på X-axeln och temperatur på Y-axeln, se figur nedan ) blir en vattenmassa till en punkt eller en liten box – blandar vi två vattenmassor kommer blandningen att ha en salthalt och temperatur som ligger på en rät linje mellan de två ursprungliga vattenmassorna.
Uppgift 1
Du har två flaskor A och B med havsvatten där \(S_A\)=33.2, \(T_A\)=4C och \(S_B\)=34.8, \(T_B\)=1C. Rita in dem i ett TS-diagram.
a) Vilken salthalt och temperatur har en blandning som betår av 50% A och 50% B ?
b) Vilken salthalt och temperatur har en blandning som betår av 10% A och 90% B ?
c) Vilken salthalt och temperatur har en blandning som betår av 73% A och 27% B ?
d) Rita in dina blandingar i TS-diagramet. Vad ser du?
e) Om du har en tredje vattenmassa där \(S_C\)=33.7, \(T_A\)=0C – vilka blandningar kan du få då?
Uppgift 2
Läs in och plotta temperatur och salthalt från Riggen S4, 320 m djup som en funktion av tid (Filen heter: Riggdata_S4_TS.txt).
a) Tiden är given i dagar sedan 1 Januari 2012. Vilken dag sattes riggen ut? När togs den in?
b) Vad är medel temperatur/salthalt och standard avvik?
c) Ser du någon sässongsvariation? Kan den beskrivas med en sinusfunktion? Varför / varför inte?
d) Plotta nu temperatur som en funktion av salthalt, vad ser du? Kan du beskriva förhållandet mellan salt och temperatur med hjälp av linjär regression?
e) Ett instrument i närheten mätte S=34.25 , S=34.6 och S= 33.9 – vad tror du temperaturen var?
f) Är dina svar på uppgiften ovan rimliga? Havsvatten fryser vid -1.9C. För vilka salthalter är din regression giltig?
g) Observationerna visar att vattnet vi observerar vid riggen är en blandning av CDW (Circumpolar Deep Water) och WW (Winter Water). Vilka egenskaper har vårt CDW? WW har vanligtvis en temperatur på -1.9C. Observerar vi rent WW på riggen? Använd regressionen till att bestamma vilken salthalt WW har.
h) Du har nu bestämt egenskaperna (S och T) på WW och CDW. Vilken temperatur och salthalt får en blandning utav 10% CDW och 90%WW? 50% av varje? 75% CDW och 25% WW?
i) Vilken temperatur har vatten som har en salthalt på 34.45? Hur stor del av vattnet är CDW och WW?
Uppgift 3
Vattnets densitet – dvs hur mycket 1 m\(^3\) vatten väger – beror på vilken temperatur och vilken salthalt det har. Kallt vatten är tyngre än varmt, färskt vatten är lättare än salt. Sambandet mellan S, T och densitet är komplicerat, men för små ändringar i salt och temperatur så är förhållandet tillnärmat linjärt:
\( \rho = \rho_0 [1 + \beta (S – S_0) – \alpha (T – T_0) ] \)
I utrykket over er \(S\) saltholdighet, \(T\) er temperatur, \(\beta\) er den haline koeffisienten og \(\alpha\) er den termale koeffisienten. \(S_0\) och \(T_0\) är referensvärden som man själv kan välja och \(\rho_0=\rho(S_0,T_0)\). Värdena på \(\alpha\) och \(\beta\) beror på vilka värden du väljer för \(S_0\) och \(T_0\). Om vi väljer \(S_0\)=34.6 og \(T_0=\)=0.5C så är \(\rho_0=\rho(S_0,T_0)\)=1027,8 kg/m\(^3\), \(\alpha \approx \) 5.77*10\(^{-5}\) C\(^{-1}\) och \(\beta \approx 7.84*10^{-4}\). Med andra ord så utgår vi från ett referansvärde och så beräknar vi bidraget från ändringar i salt och temperatur.
Använd linjäriseringen till att beräkna densitetsprofilre från temperatur och salt profilerna i CTDdata_Amundsenhavet.txt. Hur ser de ut i jämförelse med profilerna för salt och temperatur?
a) Välj en av profilerna. Var är densiteten störst? minst? varför är det så?
b) Hur stor är densiteteskillnaden mellan ytan och botten? Hur mycket saltare måste vattnet i ytan bli för att det ska bli lika tungt som vattnet på bottnen?
Densiteten måste öka med ökande djup, annars är vattnet instabilt: tungt vatten ligger vanpå lätt vatten. Det tunga vattnet kommer då att sjunka ned till “`sin”‘ nivå (Det kallas konvektion) .
c) Om vi kyler ner vattnet i ytan till fryspunkten (\( T_f \)=-1.9C), hur tungt blir det då? Vad tror du händer?
När det blåser så blandas vattnet i ytan om och vi får ett homogen (konstant salthalt och temperatur) lag på toppen. Då blir den nya salthalten i ytan lik medelsalthalten av det vatten som blandats om.
d)Vad är medelsalthalten i den översta 100 m?
e)Hur tungt blir det homogena lagret i ytan om det kyls ner till fryspunkten? (\(T_f\)=-1.9C)
f) Hur mycket måste vi öka salthalten för att vattnet ska bli lika tungt som vattnet på botten? Hur kan salthalten öka i Antarktis? I Medelhavet?
Uppgift 4
När vattnet blir varmare sjunker densiteten – det betyder att varmt vatten tar mer plats. En stor del av höjningen i havsnivån som vi ser idag (och kommer att se mer av i framtiden) beror på att vattnet nere i djupet värms upp. Om 4000 m djupt vatten (med \( S_0 \) , \( T_0 \) , \( \rho_0 \) , \( \beta \) och \( \alpha \) som i uppgift 3) värms upp en grad, hur mycket stiger havsnivån då?
Uppgift 5
När det fryser is, så är det vattenmolekylerna som bildar kristaller och blir till is. Största delen av saltet skiljs ut och blandas in i vattnet under. Salthalten* på ganska ny is är typiskt 7-10**. Eftersom salthalten har så stor betydelse för vattnets densitet, vill vi gärna veta hur mycket salthalten ökar i vattnet ( \( \Delta S \)) om det fryser is med en viss tjockelse (\(h_{is}\)) och salthalt (\(S_{is}\)). Det kan vi räkna ut med formeln
\(\Delta S= \frac{h_{is}(S-S_{is})}{H_{vatten}}\)
där \(H_{vatten}\) är tjockleken på lagret med vatten som saltet blandar sig i.
a) Hur mycket ökar salthalten om vi fryser (i) 10 cm (ii) en meter med is över ett 100 m tjock lager där S=34.5 och \(S_{is}\)=7.
b)Hur mycket ökar salthalten om vi fryser (i) 10 cm (ii) en meter med is över ett 1000 m tjock lager där S=34.5 och \(S_{is}\)=7.
c) Hur mycket ökar densiteten i a-b? Låt T=T\(_f\) (Se uppgift 3).
d) Hur mycket is måste vi frysa för att vattnet i uppgift 3h ska bli lika tungt som vattnet på bottnen? (Låt H=100 m, tjockleken på lagret som stormen rörde om). Är det realistiskt?
*Man bestämmer salthalten på is genom att smälta ner den och mäta salthalten på smältvattnet
** På gammal is i Arktis kan den vara nästan 0!
