
Vi oseanografer snakker ofte om «vannmasser». Dette er vann med ulikt opphav og som derfor har ulik saltholdighet og temperatur. Vi snakker for eksempel om Atlantisk vann som er varmt og salt, om Antarktisk overflatevann som er kaldt og ferskt, og om Antarktisk sokkelvann som er kaldt og salt. Vannets saltinnhold og temperatur bestemmer dets tetthet; kaldt vann er tyngre enn varmt vann, ferskt vann er letter enn salt.
Det er i stor grad atmosfæren som bestemmer vannmassenes egenskaper. Der det er varmt varmes opp, der det er kaldt kjøles det ned. Saltholdigheten bestemmes av fordampning, ferskvannstilførsel (fra elver og bekker eller fra regn eller snø), og av isdannelse. Når det dannes is om vinteren, er det vannmolekylene som fryser. Det meste av saltet blir skilt ut, og saltholdigheten i vannet under øker. I grunne områder der det dannes mye is – for eksempel på noen av kontinentalsoklene i Antarktis – kan vannet bli veldig salt og dermed veldig tungt. Når isen senere smelter om våren så dannes det et ferskt lag på toppen av det salte. I oppgaven her snakkes det om “Circumpolar Deep Water”, CDW. CDW er egentlig en blanding av flere vannmasser, blant annet vann som kommer helt fra Nord-atlanteren. CDW har en temperatur mellom 1 og 2 grader og en saltholdighet mellom 34.62 og 34.73. Saltholdigheten har merkelig nok ingen enhet, men det tilsvarer omtrent promille. Om saltholdigheten er 1 så er det 1 gram salt per kilo vann. Saltholdigheten i havet er typisk 35, eller ca. 3,5%.
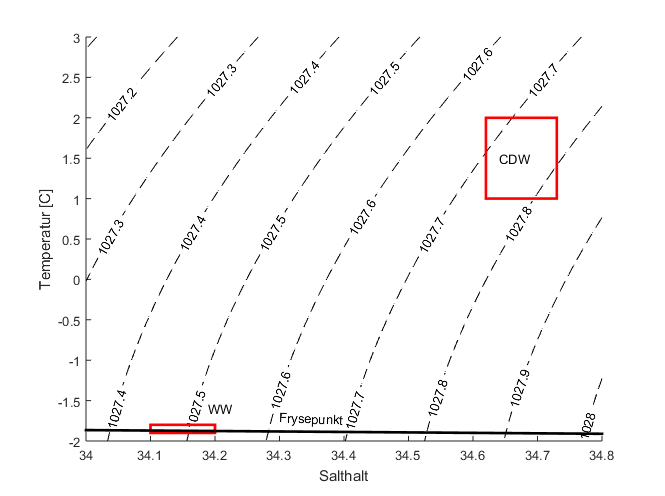
I et TS-diagram (en figur med saltholdighet på x-aksen og temperatur på y-aksen; se figur) blir en vannmasse til et punkt eller en liten boks. Blander vi to vannmasser kommer blandingen til å ha en saltholdighet og en temperatur som ligger på rett linje mellom de to originale vannmassene.
Oppgave 1
Du har to flasker A og B med havvann der \(S_A\)=33.2, \(T_A\)=4C og \(S_B\)=34.8, \(T_B\)=1C. Tegn dem inn i et TS-diagram.
a) Hvilken saltholdighet og temperatur har en blanding som består av 50% A og 50% B ?
b) Hvilken saltholdighet og temperatur har en blanding som består av 10% A og 90% B ?
c) Hvilken saltholdighet og temperatur har en blanding som består av 73% A og 27% B ?
d) Tegn inn dine blandinger i TS-diagrammet.Hva ser du?
e) Om du har en tredje vannmasse der \(S_C\)=33.7, \(T_A\)=0C – hvilke blandinger kan du få da?
Oppgave 2
a) Les inn og plott temperatur og saltholdighet fra riggen S4, 320 m dybde som en funksjon av tid (Filen heter: Riggdata_S4_TS.txt).
b) Tiden er gitt i dager siden 1. Januar 2012. Hvilken dag ble riggen satt ut? Når ble de tatt opp igjen?
c) Hva er middel temperatur/saltholdighet og standardavvik?
d) Ser du noen sesongvariasjon? Kan den beskrives med en sinusfunksjon? Hvorfor / hvorfor ikke?
e) Plott temperatur som en funksjon av saltholdighet, hva ser du? Kan du beskrive forholdet mellom salt og temperatur med hjelp av lineær regresjon?
f) Et instrument i nærheten målte S=34.25, S=34.6 og S= 33.9 – hva tror du temperaturen var?
g) Er dine svar på oppgaven ovenfor rimelige? Havvann fryser ved -1.9C. For hvilke saltholdigheter er din regresjon gyldig?
h) Observasjonene viser at vannet vi observerer ved riggen er en blanding av CDW (Circumpolar Deep Water) og WW (Winter Water). Hvilke egenskaper har vårt CDW? WW har vanligvis en temperatur på -1.9C. Observerer vi rent WW på riggen? Bruk regresjonen til å bestemme hvilken saltholdighet WW har.
i) Du har nå bestemt egenskapene (S og T) på WW og CDW. Hvilken temperatur og saltholdighet får en blanding av 10% CDW og 90%WW? 50% av begge? 75% CDW og 25% WW?
j) Hvilken temperatur har vann som har en saltholdighet på 34.45? Hvor stor del av vannet er CDW og WW?
Oppgave 3
Vannets tetthet – dvs. hvor mye 1 m\(^3\) vann veier – er avhengig av hvilken temperatur og hvilken saltholdighet det har. Kaldt vann er tyngre enn varmt, ferskt vann er lettere enn salt. Sammenhengen mellom S, T og tetthet er komplisert, men for små endringer i salt og temperatur så er forholdet tilnærmet lineært:
\( \rho = \rho_0 [1 + \beta (S – S_0) – \alpha (T – T_0) ] \)
I utrykket over er \(S\) saltholdighet, \(T\) er temperatur, \(\beta\) er den haline koeffisienten og \(\alpha\) er den termale koeffisienten. \(S_0\) og \(T_0\) er referanseverdien som man selv kan velge og \(\rho_0=\rho(S_0,T_0)\). Verdiene på \(\alpha\) og \(\beta\) avhenger av hvilke verdier du velger for \(S_0\) og \(T_0\). Om vi velger \(S_0\)=34.6 og \(T_0=\)=0.5C så er \(\rho_0=\rho(S_0,T_0)\)=1027,8 kg/m\(^3\), \(\alpha \approx \) 5.77*10\(^{-5}\) C\(^{-1}\) og \(\beta \approx 7.84*10^{-4}\). Med andre ord så starter vi fra en referanseverdi og så beregner vi bidraget fra endringer i salt og temperatur.
Bruk lineariseringen til å beregne tetthetsprofiler fra temperatur og salt profilene i CTDdata_Amundsenhavet.txt. Hvordan ser de ut sammenlignet med profilene for salt og temperatur?
a) Velg en av profilene. Hvor er tettheten størst? minst? Hvorfor er det slik?
b) Hvor stor er tetthetsforskjellen mellom overflaten og bunn? Hvor mye saltere må overflatevannet bli for at det skal bli like tungt som vannet på bunn?
Tettheten må øke med økende dyp, ellers er vannet ustabilt: tungt vann ligger over lett vann. Det tunge vannet kommer da til å synke ned til «sitt» nivå (noe som kalles konveksjon).
c) Om vi kjøler ned vannet i overflaten til frysepunktet \((T_f\)=-1.9C), hvor tungt blir det da? Hva tror du skjer?
d) Når det blåser så blandas vannet i overflaten og vi får ett homogent (konstant saltholdighet og temperatur) lag på toppen. Da blir den nye saltholdigheten i overflaten lik middelsaltholdigheten til det vannet som blandes.
e) Hva er middelsaltholdigheten i de øverste 100 m?
f) Hvor tungt blir det homogene laget i overflaten om det kjøles ned til frysepunktet? (\(T_f\)=-1.9C)
g) Hvor mye må vi øke saltholdigheten for at vannet skal bli like tungt som vannet på bunnen? Hvordan kan saltholdigheten øke i Antarktis? I Middelhavet?
Oppgave 4
Når vannet blir varmere synker tettheten – det betyr at varmt vann tar mer plass. En stor del av havnivåstigningen som vi ser i dag (og kommer å se mer av i framtiden) skyldes at vannet nede i dypet varmes opp. Om 4000 m dypt vann (med \(S_0\), \(T_0\), \(\rho_0\),\(\beta\) og\(\alpha\)) som i oppgave 3 varmes opp en grad, hvor mye stiger havnivået da?
Oppgave 5
Når det fryser is, så er det vannmolekylene som danner krystaller og blir til is. Største delen av saltet skilles ut og blandas inn i vannet under. Saltholdigheten* på ganske ny is er typisk 7-10**. Ettersom saltholdigheten er så viktig for vannets tetthet, vil vi gjerne vite hvor mye saltholdigheten øker i vannet (\(\Delta S\)) om det fryser is med en viss tykkelse (\(h_{is}\)) og saltholdighet (\(S_{is}\)). Det kan vi regne ut med formelen:
\(\Delta S= \frac{h_{is}(S-S_{is})}{H_{vann}}\)
der \(H_{vann}\) er tykkelsen på laget med vann som saltet blander seg med.
a) Hvor mye øker saltholdigheten om vi fryser (i) 10 cm (ii) en meter med is over et 100 m tykt lag der S=34.5 og \(S_{is}\)=7.
b) Hvor mye øker saltholdigheten om vi fryser (i) 10 cm (ii) en meter med is over et 1000 m tykt lag der S=34.5 og \(S_{is}\)=7.
c) Hvor mye øker tettheten i a-b? La T=T\(_f\) (Se oppgave 3).
d) Hvor mye is må vi fryse for at vannet i oppgave 3h skal bli like tungt som vannet på bunnen? (La H=100 m, tykkelsen på laget som stormen blandet). Er det realistisk?
*Man bestemmer saltholdigheten på is ved å smelte den og deretter måle saltholdigheten på smeltevannet.
** På gammel is i Arktis kan den være nesten 0!
