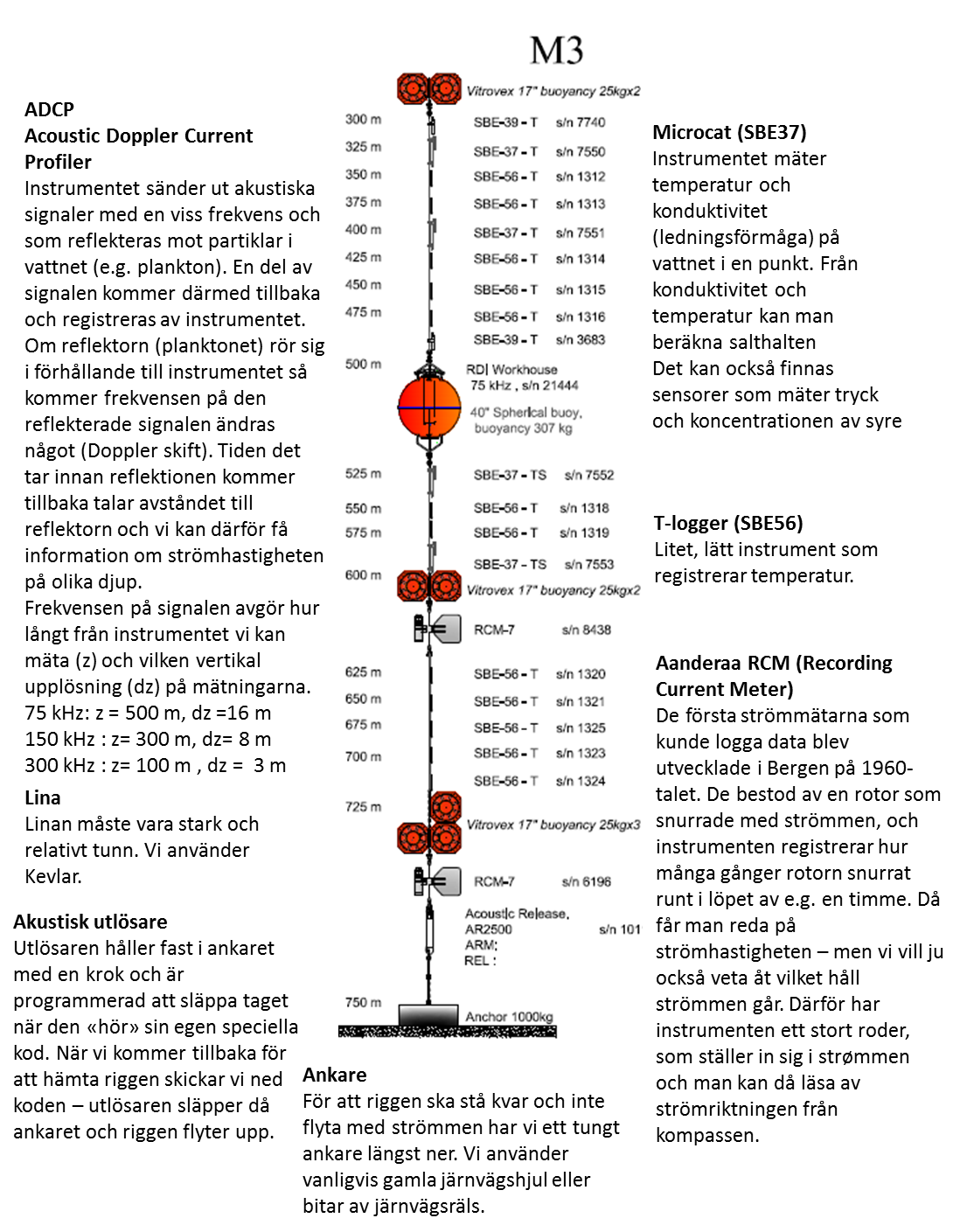
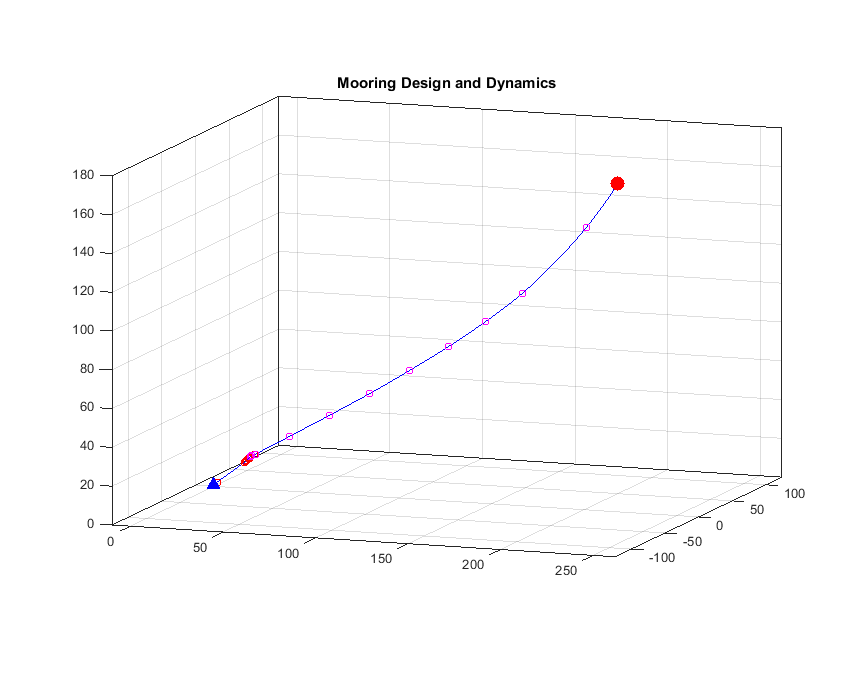
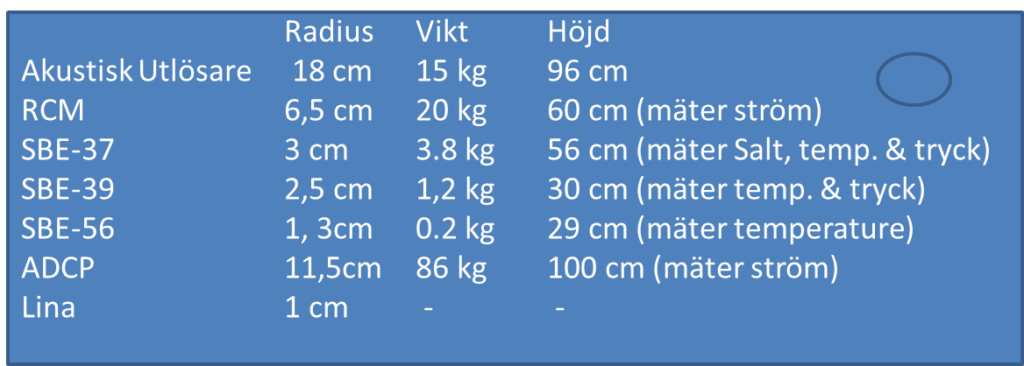
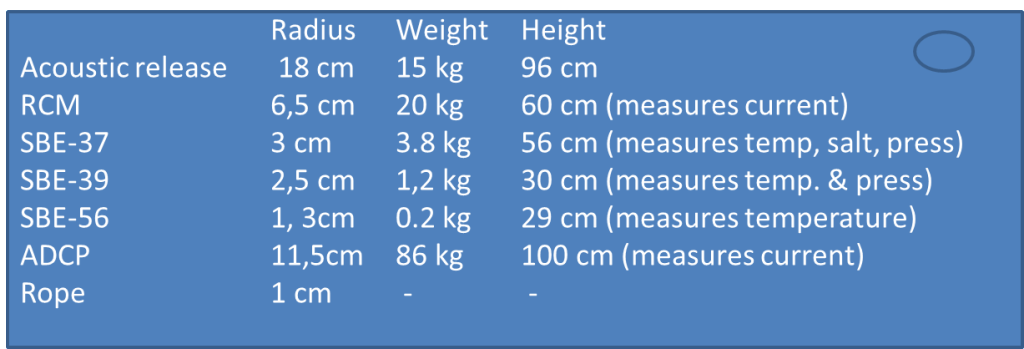
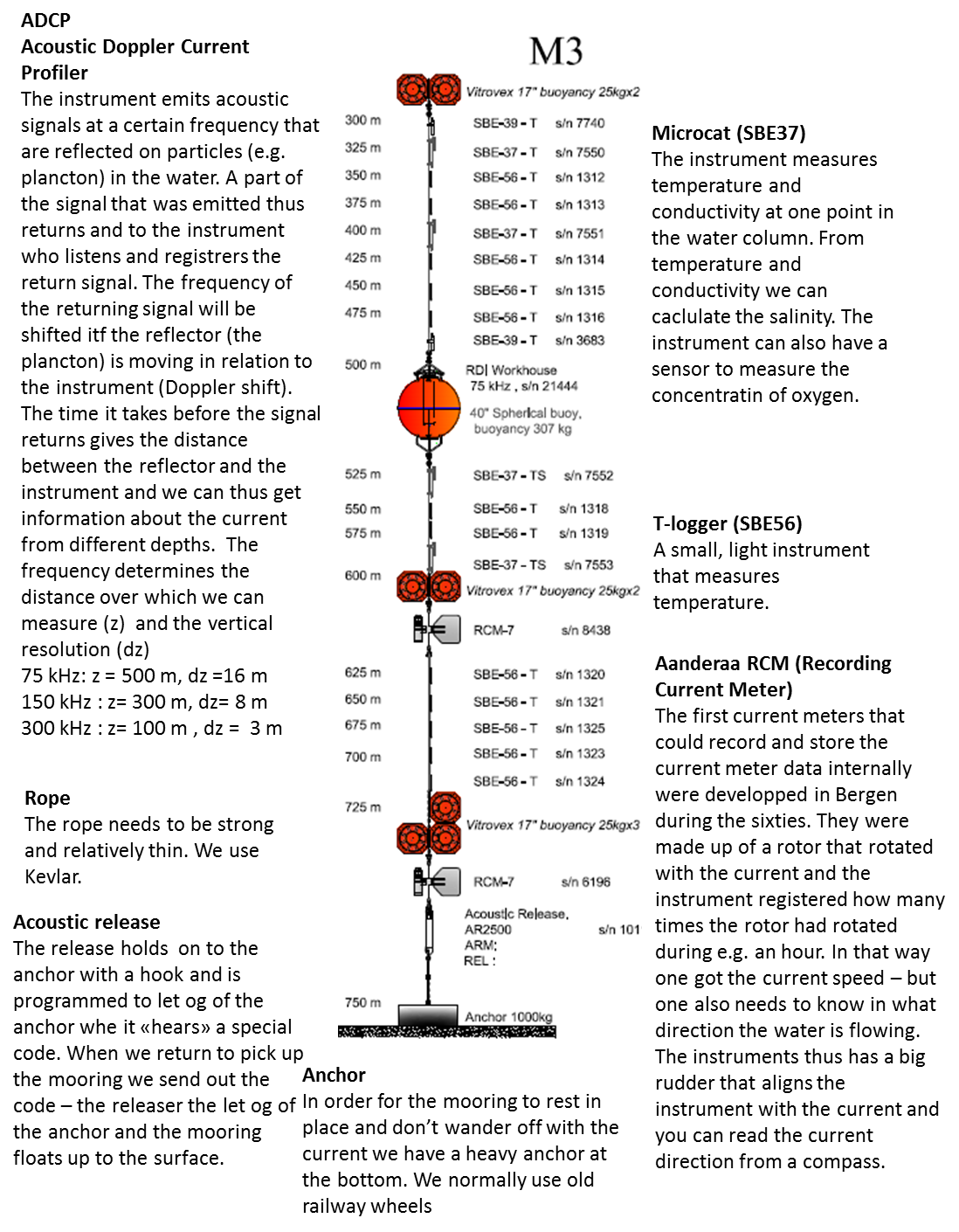
Med CTD och LADCP (strömmätare som sitter på CTD:n) får vi reda på hur vattnet strömmar och vilken temperatur det har just nu, när vi är här – men vi vill så klart också veta vad som händer när vi rest hem igen. Därför sätter vi ut instrumenter på så kallade riggar som kan stå kvar och mäta när vi åkt hem, och så kan vi komma tillbaka och hämta dem senare. Jag har aldrig varit i Amundsenhavet tidigare, så jag har inga riggar att plocka upp jag ska bara sätta ut nya. Mina svenska, engelska och Koreanska kollegor har riggar i vattnet – och det var med stor spänning vi tidigare i veckan närmade oss platsen där en av dem för två år sen sattes ut. Karen skickade hydrofonen över relingen och ner i vattnet och knappade in utlösarens speciella kod. Långt under oss nere på botten stod den och väntade snällt på att få höra från oss – och när den efter två år nu äntligen gjorde det så svarar den glatt “jag är här!”. Karen knappade in en ny kod som betyder “släpp”, och snart fick hon ett nytt svar “jag har släppt, jag är på väg upp!”. Alla spejade ut i dimman – ivriga att vara den första som fick syn på de gula bojarna.
– Där är den! Där borta!
Besättningen är snabbt ut i en mindre båt för att börja arbetet med att plocka upp riggen – de vet vad de ska göra, det här har de gjort förr. Några timmar senare är alla instrument ombord och vi arbetar för fullt. All data ska lastas över från instrumenten till datorer och hårddiskar, sedan ska instrumenten gås över och få nya batterier och programmeras. Imorgon ska de ner i vattnet igen!
Koreanerna hade inte lika tur; deras första rigg hade gått av en bit ovanför botten och det var bara utlösare och ett par temperatursensorer som kom upp. Deras andra rigg var helt borta – troligtvis är det ett stort isberg som dragit den med sig. Men de sista tre kom upp som på beställing!

I går hade vi möte med besättning och tekniker för att gå igenom hur mina riggar ser ut och för att bestämma hur vi bäst sätter ut dem. Besättningen talar dålig eller ingen engelska*, så mötet hölls på koreanska – och bara då och då kom det en fråga på engelska till mig. I en knapp timme lät det ungefär så här:
ㄻㅊ널촘ㅈ괴ㅓㄴ모거모 ㅏㄱ mooring ㅓ로ㅕ추마 ADCP ㅕ루 멍로 ㅏㅕ고러ㅏㅓ Shackleㄷ ㅣ찰머놀ㄹ러ㅏmooring 몬염ㅍ뒤곤?mooring름 ㅡㅐㅐA-frame 갸ㅜㅎ 멀촘너 .

Jag har i lugn och ro förberett mina instrumenter och min utrustning – i tron om att det fortfarande var flera dagar kvar tills de skulle i vattnet. Koreanerna hade fyra riggar kvar att sätta ut först. Men så blåste det upp och helt plöstligt gick vågorna höga – och kaptenen gav order om att det var för farligt att arbeta på däck… så nu har de vänt hela arbetsschemat på huvudet och vi kör med full fart västerut, till västra delen av Getz shelfis. Där är det mer is och förhoppningsvis mindre vågor, och desutom kan vi då använda tiden med dåligt väder till att förflytta oss, istället för att ligga och vänta på att vi ska kunna sätta ut riggar. Så nu är det helt plöstligt min sista rigg som står överst på dagordningen …och jag har tyvärr inte tid att skriva mer till er just nu!
*Jag frågade La, en av oceanograferna som pratar bra engelska var han lärt sig språket. De andra som pratar bra engelska har alla gjort doktorgrad eller bott utomlands – men jag visste att han inte har gjort det. Efter en stund kom det fram att han under studietiden en gång i veckan pratat engelska med de enda i Korea som är villiga att prata engelska med dig helt gratis: Jehovas vittnen och mormoner! “Men jag är fortfarande Buddhist, jag ville bara lära mig prata engelska och hade inte råd med privat lärare…”
Oppgaver og øvelser
Norsk
Svenska