Vi reser på tokt till Amundsenhavet vartannat år då gör vi en massa mätningar och får en bild av vad som händer just då, när vi är där. Men vi vill ju såklart också veta vad som händer när vi inte är där. Därför sätter vi ut “riggar”. Riggar är kort och gott ett ankare, en lina som vi sätter fast instrumenter på och så flytelementer som håller den uppe. Riggen får stå kvar på botten och mäta (vanligtvis ström, salt och temperatur men jag ska också ha instrumenter som mäter koncentrationen av syre i vattnet) tills vi kommer tillbaka ett år eller två senare för att hämta upp den. Hur riggen ser ut och vilka instrumenter man sätter på den beror så klart på vad man ska studera! I tabellen i uppgift 2 ser du några av instrumenten vi använder och her ser du hur en av mina riggar ska se ut:
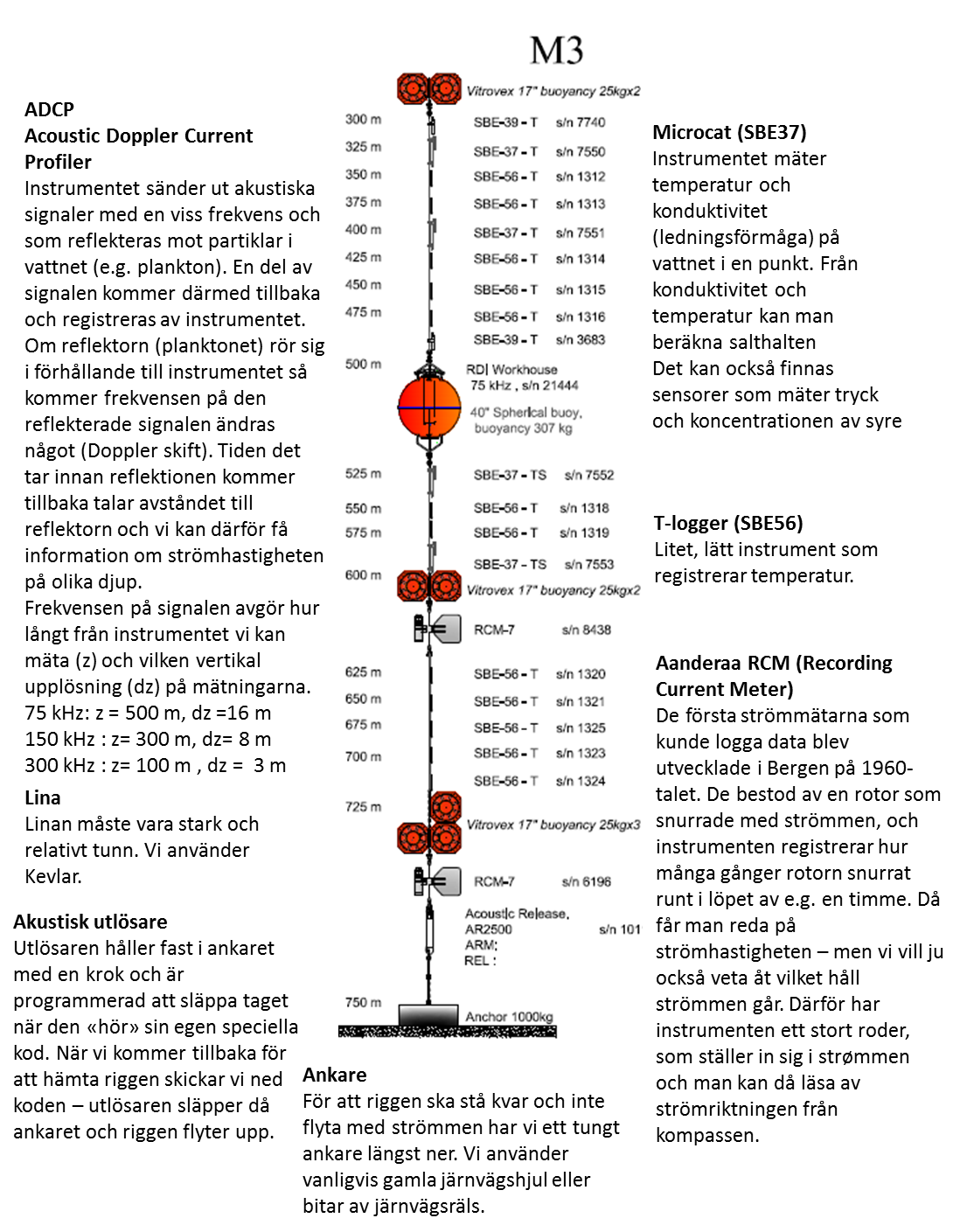
Uppgift 1
Nu kan du få designa din! Hur skulle din rigg sett ut om du vill
- studera hur vattnets salthalt och temperatur förändrar sig i de övre 200 m under ett år i ett område som är 500 m djupt?
- studera en bottenström som når upp till 300 m över botten?
- ta reda på hur mycket varmt vatten som strömmar in under in shelfis? Det är 800 m djupt. Tänk på att isbergen kan nå ner till 300 m djup!
Uppgift 2
Gör beräkningarna för din egen rigg eller för en rigg som har:
1 x Utlösare (25 möb); 3 x SBE37 (25, 150 och 300 möb), 1 x RCM (50 möb), 1 x ADCP (300 möb) och 5 x SBE56 (50, 75, 100, 200, 250 möb). Möb=meter över botten.
Instrumenterna har följande dimensioner (alla har omtrent sylinderform):
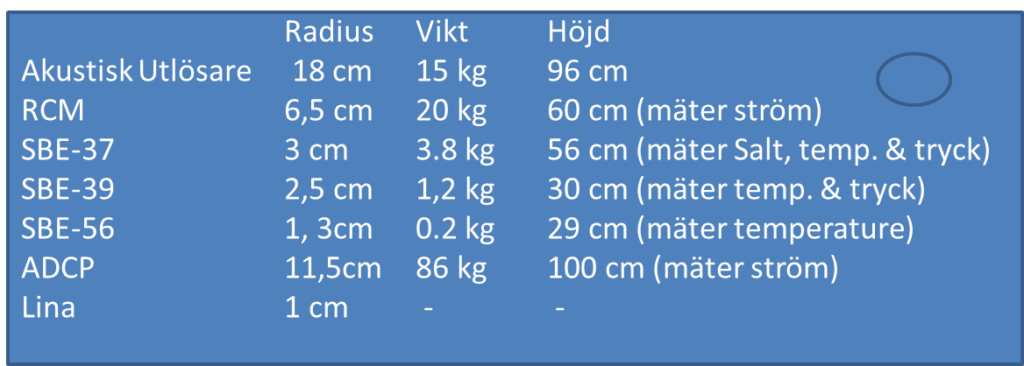
a) Hur mycket väger instrumenterna på riggen i luft? i vatten?
Riggen måste också ha flytelementer (glaskulor) för att stå vertikalt!
b) Hur stor är uppdriften från en glaskula? Glaskulornas diameter är 43 cm och de väger 22 kg (i luft).
c) Hur många glaskulor behöver vi för att hålla riggen uppe?
Uppgift 3
När det är stark ström så dras riggen ner mot botten – det är inte bra. För det första får man inte mätningar från de djup man hade tänkt och för det andra så kan många instrument inte mäta när de lutar för mycket. En ADCP kan till exempel inte mäta strömmen om den lutar mer än 15\(^\circ\). Därför sätter vi på extra flytelementer för att hålla riggen upprätt också när det är stark ström. Kraften som det strömmande vattnet utövar på riggen är proportional mot arean som vattnet träffar.
a) Hur stor andel av riggens “area” utgör linan?
b) Hur mycket minskar motståndet om vi bytar till en lina som bara är 6 mm i diameter?
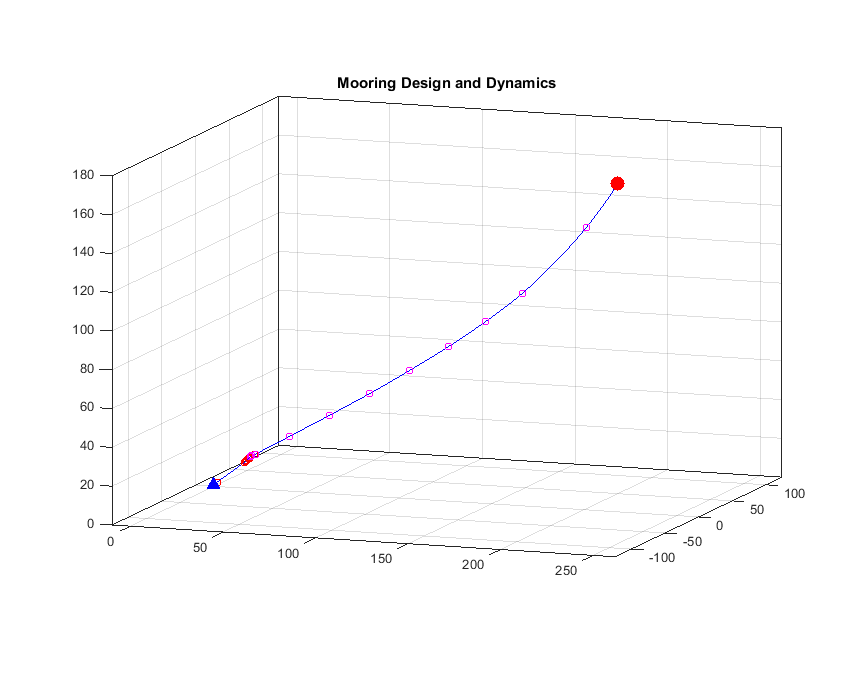
c) Ett instrument har dragits ned till 170 m över botten (möb) och dragits 218 meter nedströms, ett annat instrument har dragits ned till 65 mab och dragits 105 meter nedströms. Formen på linan kan beskrivas med en (halv) parabel. Finn uttrycket för parabeln!
d) Trycksensorn på en ADCP visar att den nu sitter 40 m över botten. Hur mycket lutar den då? Kan vi använda mätningarna?
e) Hur högt upp måste ADCP ha suttit för att vi skulle kunnat använda mätningarna?
f) Varför tror du vi hellre sätter en ADCP högt uppe så att den tittar ner, hellre än att den sitter närma botten och tittar upp?
Uppgift 4
När vi hämtar upp riggen igen och lastar ner datan från instrumenterna så får vi tidserier av ström, temperatur och salthalt. Nu ska vi titta på data från riggar som stod ute i Amundsenhavet 2012.
a) Läs in och plotta strömmätningarna från rigg S4 i 17-24 juni, 2012. (Riggdata_S4_1). Strömmätningarna är i cm/s. Vad är det vi ser?
b) Hur stor är medelströmmen? i vilken riktning går den? (\(u\) ger strömstyrkan i \(x\)-riktning (mot öst) och \(v\) ger strömmen i \(y\)-riktning (mot norr))
c) Om du ska tillpassa eller beskriva observationerna med en funktion, vilken väljer du då?
d) Bestäm konstanterna med hjälp av regression.
e) Ett isberg flyter med strömmen i närheten av S4 – sätt upp ett uttryck (på vektorform) för hur isberget kommer att förflytta sig och plotta trajektorien i en ny figur. Beskriv rörelsen!
f) Plotta strömmen en vecka fram i tiden med hjälp av din funktion från (d).
g) Läs in datan från S4 24/6 – 1/7 och plotta den i samma figur – stämmer din model? Varför/varför inte? (Filen heter: Riggdata_S4_2)
Uppgift 5
Läs in och plotta tryckmätningarna från rigg C2. Här var strömmen mycket starkare än vad vi trodde, och vi hade inte satt på tillräckligt med flytelementer 🙁 (Filen heter: Riggdata_C2)
a) Vad är det vi ser? (hint: se uppgift 2)
b) Hur djupt sitter instrumentet när det är svag ström? (1 m \(\approx\) 1 dbar)
c) Hur djupt dras det ned maximalt?
d) Hur stor del av tiden har det dragits ner mer än 40 m? 80 m?
e) \(u\) ger strömstyrkan i \(x\)-riktning (mot öst) och \(v\) ger strömmen i \(y\)-riktning (mot norr). Använd Pythagoras sats och sätt upp ett uttryck för strömstyrkan. Räkna så ut den! Hur stark är den starkaste strömmen? medelströmmen? Hur många kilometer/timme är det?
f) Är det något samband mellan strömstyrka och tryck (dv neddragning)? Hur ser det ut? Beskriv sambandet matematiskt och förklara med ord!
Uppgift 6
Instrumenten går på batteri – och varje gång de gör en mätning går det åt lite (eller mycket om det är en ADCP) energi. Vi vill såklart att instrumenten ska göra mätningar helt tills vi kommer tillbaka och hämtar dem – så vi räknar i förväg ut hur ofta vi kan göra mätningarna utan att batteriet tar slut. Men vi måste också ta hänsyn till e.g. tidvatten när vi bestämmer hur ofta vi ska mäta.
a)Det dagliga tidvattnet (en av komponenterna) har en period på 25.8h. Tidvattnet kan beskrivas med en sinus kurva. Amplituden (och fasen) beror på var vi är – men anta att amplituden är 10 cm/s och fasen 0. Sätt upp ett uttryck som beskriver tidvattnet och plotta det trettio dagar fram i tiden.
b) Om vi gjort mätningar bara en gång om dagen (i.e. var 24 h), hur hade vår tidserie sett ut då?
c) Vilken period har «svängningen» som vi då observerat?
d)Tidvattnet som vi observerar är en summa av många tidvattenskomponenter med olika perioder. En annan heldaglig tidvattenskomponent har en period på 23.93h. Sätt upp uttrycket för den tidvattenskomponenten om amplituden är 9 cm/s (fasen kan du sätta till noll) och plotta summan av de två komponenterna. Vad är det du ser? Hur ändras amplituden? Hur långt är det mellan två «amplitudmaximum»? Kan du förklara vad som sker? (tips – plotta både de enskilda komponenterna och summan av dem). Jämför resultatet med dina resultat från uppgift 3g!
