
Is, is, is! Det är is överallt! Stora isflak, små isflak och så ett och annat isberg. Det är vitt och vackert… men framförallt så är det slut på vågor och sjösjuka! Isen tar effektivt död på vågorna.
När vi tar värme från havet, så kyls det ner helt tills det når fryspunkten. Då kan det inte kylas ner mer… fortsätter vi att ta bort värme, så fryser det is. Den värme vi tar bort är då den latenta värmen som frigörs när vattnet blir till is. Nu är det ju inte “vi” som tar bort värme utan atmosfären. När luften är kallare än vattnet, så försvinner värme från vattnet upp i luften: ju kallare det är, ju fortare försvinner värmen. Ju kallare det är ju fortare växer isen. Men isen är en god isolator, den isolerar havet från den kalla atmosfären ovanpå. Precis som jackan isolerar dig när det är kallt ute och gör att du behåller din värme så gör isen att havet förlorar mindre värme, eftersom all värme som avges till atmosfären måste ledas upp genom isen. Ju tjockare isen är, ju långsammare leds värmen upp genom isen, eftersom värmefluxen (\(F_{is}\), som anger mycket värme som leds upp genom isen per tidsenhet) är proportional med temperaturgradienten i isen.
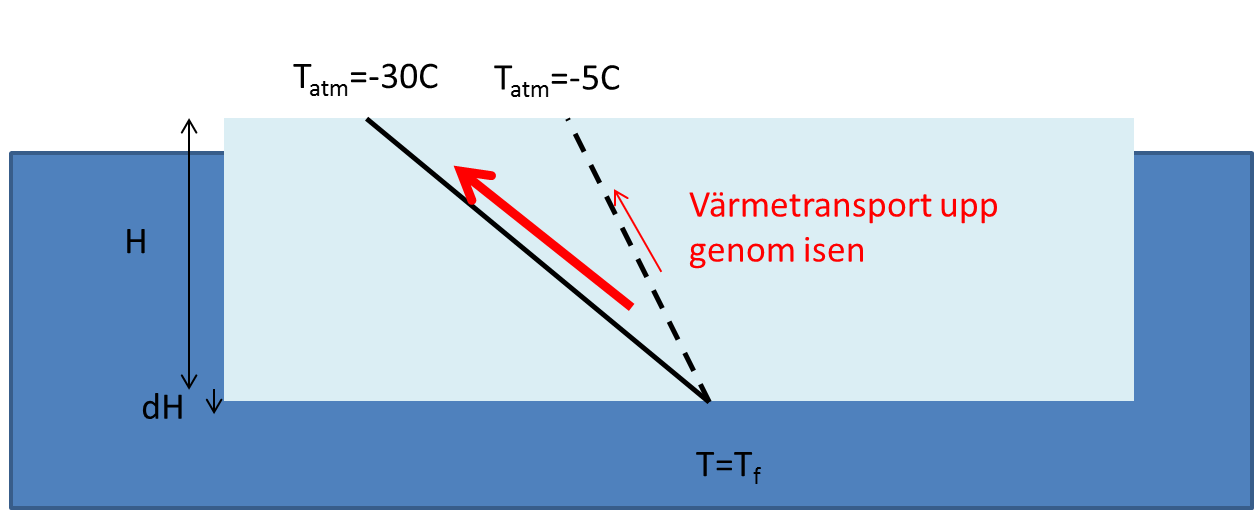
\(F_{is}=-k_{is}\frac{dT}{dz}=-k_{is}\frac{T_{atm}-T_{f}}{H}\)
\(k_{is}=2\,W\,m^{-1}\,^{\circ}C^{-1}\) är isens värmeledningsförmåga och \(H\) är tjockleken på isen. \(T_{atm}\) är temperaturen på ovansidan av isen (som vi antar är den samma som lufttemperaturen) och \(T_f=-1.9^\circ C\) är temperaturen på undersidan av isen, dvs. vattnets fryspunkt.
Den latenta värmen som frigörs (per kvadratmeter) när isen växer en pytteliten bit \(dH\) är \(\rho_{is}LdH\). Om det sker under en kort tid \(dt\) så är den latenta värmefluxen:
\(F_{latent}=\rho_{is}L\frac{dH}{dt}\)
\(\rho_{is}=900\,kg\,m^{-3}\) är isens densitet och \(L=3.3*10^5J\,kg^{-1}\) är den latenta värmen.
Isen kommer växa precis så fort all all den latenta värmen kan ledas upp genom isen, dvs så att
\(F_{latent}=F_{is}\)
När vi kombinerar de två ekvationerna så får vi en differentialekvation, som vi kan lösa för att få ett uttryck för hur istjockleken växer med tiden, \(H(t)\).
Uppgift 1
a) Sätt upp differential ekvationen og vis at uttryket för \(H(t)\) er
\(H=\sqrt{ H_0^2+\frac{2k_{is}(T_{f}-T_{atm})}{\rho_{is}L}t}\).
när \(H(t=0)=H_0\)
Tips: Bruk kjärnregelen \(\frac{dH^2}{dt}=2H\frac{dH}{dt}\).
b) Plotta funktionen för olika \(T_{atm}\)! När växer isen snabbast? Varför det? (Sätt \(H_0=0\))
c) Bruk resultatet fra (a) till att beräkna tjockleken på isen efter tio timmar efter det börjar frysa om temperaturen ute är (i) -20\(^\circ\)C (ii) -2\(^\circ\)C.
d) När isen i (c) är 1 m tjock, hur lång tid tar det då innan den har växt tio cm till?
e) Vad tror du sker när det faller snö på isen? \(\kappa_{\textit{snö}}\) är typiskt mellan 0.15 och 0.4\(W\,m^{-1}\,^{\circ}C^{-1}\). Vilket är den bästa isolatorn? Snö eller is?
f) All värme som leds upp genom isen måste också ledas upp genom snön: Var är temperaturgradienten störst? I snön eller i isen? Skissera temperaturprofilen!
Uppgift 2
Temperaturen varierar från dag till dag och från år till år. Filen Temperatur.txt innehåller temperaturdata för Amundsenhavet från mars 2014 till mars 2015.
a) Räkna ut medeltemperatur varje månad och plotta den. Räkna också ut standardavvik och rita in den i din graf. Vilken månad är kallast? varmast? när är temperaturen mest/minst variabel?
b) När slutar isen att växa?
c) Räkna ut hur mycket isen växer varje månad? Vilket värde ska du använda för \(H_0\)?
d) Plotta i) istjokleken och ii) isväxten som en funktion av tiden. När växer isen fortast? är det kallast då? varför/varför inte?

Uppgift 3
a) Om ett isflak är 30 cm tjock, 2 m brett och fem meter långt – hur stor del av isflaket sticker upp ovanför vattenytan? \(\rho_{is}=900kg m^{-3}\)
b) Hur många forskare kan stå på isflaket (i mitten) utan att bli blöta om fötterna?
c) Hur mycket snö kan falla på isen utan att isen sjunker under ytan? \(\rho_{snö}\approx 300kg m^{-3}\)
Uppgift 4
I Antarktis är isen relativt tunn och det snöar ofta så mycket att isen trycks ner under ytan av snön. Då får vi ett lager med slush (snö + havsvatten) ovanpå isen. När vattnet i blandningen fryser får vi så kallad snöis. Man uppskattar att upp mot 40% av isen i Amundsenhavet är snöis!
a) Det går fortare att frysa snöis än “vanlig” is under isflaket – kan du förklara varför? Hur långt behöver värmen ledas när vi fryser snöis? Behöver snön frysas?
