Oppgaver: Vind og vann

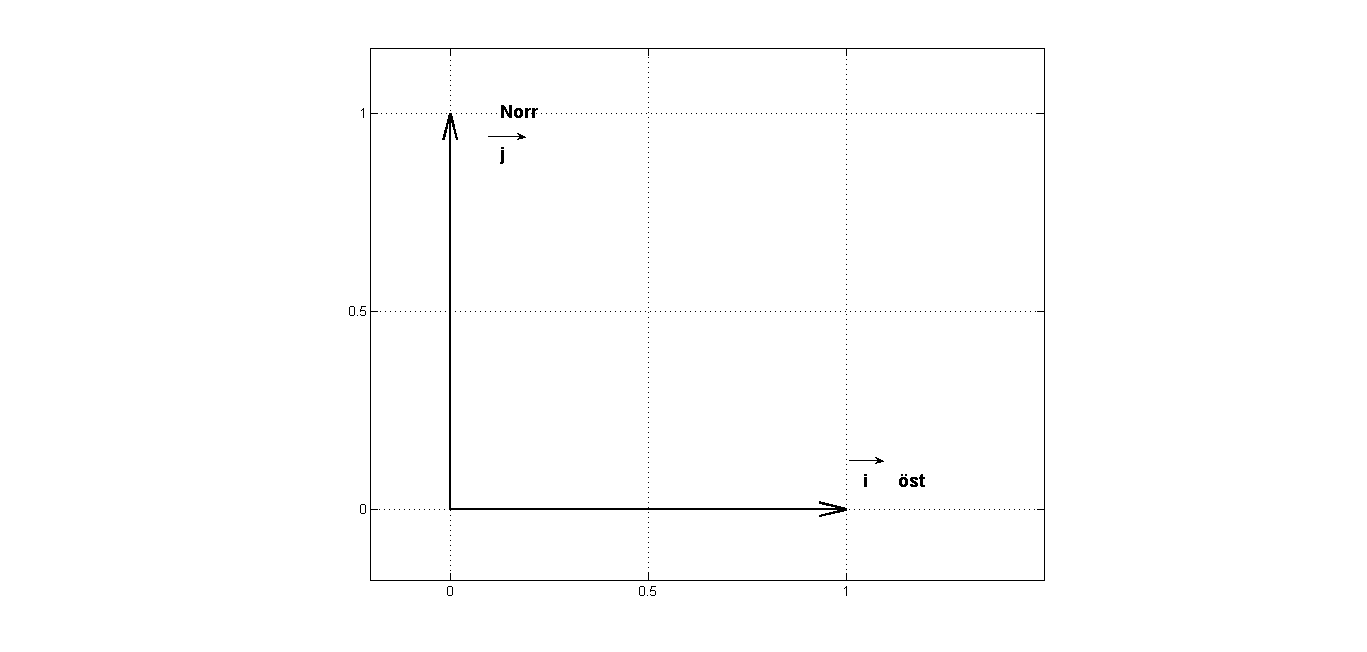
Vind og havstrømmer har en styrke og en retning, og vi bruker derfor vektorer for å beskrive dem. For eksempel er \(\vec{u}=u\vec{i} + v\vec{j}\). \(\vec{i}\) og \(\vec{j}\) enhetsvektorer som peker mot øst og nord (se figur under), mens \(u\) og \(v\) angir lengden på vektoren eller styrken på strømmen i den retningen. Om vinden blåser mot nord med 10 m/s så er \(\vec{u}=10\vec{i}\); blåser den mot sør så er \(\vec{u}=-10\vec{i}\); og blåser den mot nordøst så er \(\vec{u}=7.1\vec{i}+7.1\vec{j}\).

Isforholdene forandrer seg hele tiden på grunn av vind og havstrømmer. Så kapteinen må hele tiden følge med og se på for eksempel satellittbilder slik at vi ikke blir «fanget» av drivisen. Araon er en isbryter, men å bryte is går sent og bruker mye drivstoff. Havisen er relativt tynn og påvirkes mest av vinden. En tommelfingerregel er at isen forflytter seg med ca 2% av vindhastigheten og ca 30 grader til venstre for vinden (til høyre i Arktis).

 

Oppgave 1

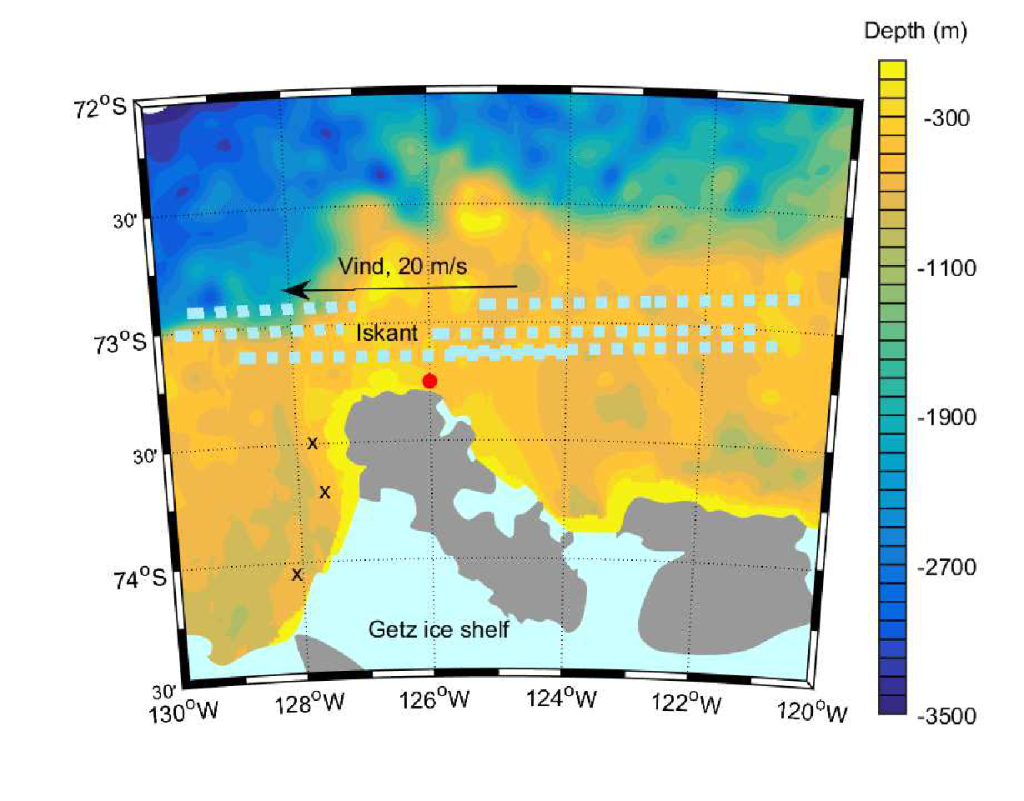
Vinden blåser 20 m/s mot vest og iskanten er 5 km fra land

a) Uttrykk vinden og isens bevegelse i vektorformat!

b) Hvor langt sørover forflytter isen seg på en time?

c) Hvor fort må Araon kjøre for å komme forbi odden (se figur) inne isen stenger passasjen? Klarer vi det?

Oppgave 2

Vinden utøver et stress \((\vec{\tau}=\tau_x\vec{i} + \tau_y\vec{j})\) på vannoverflaten og setter opp en strøm i vannet. Stressets størrelse kan vi regne ut fra vinden: \(\vec{\tau}=C_{D}\left|\vec{u}\right|\vec{u}\), der \(\vec{u}=u\vec{i}+v\vec{j}\) er vinden i 10 m høyde.

a) Om det blåser 10 m/s mot nord og \(C_D=1.6\times10^{-3}\), hvor stort er stresset da? I hvilken retning virker det?

b) Man vet at størrelsen på \(C_D\) endres når det er is på vannet, og noen forskere har foreslått at \(C_D=10^{-3}\times(1.5+2.233C_i-2.333C_i^2)\) der \(C_i\) er andelen av havoverflaten som er dekket av is (iskonsentrasjonen). For hvilken iskonsentrasjon er \(C_D\) størst? Minst? Hvor stor var iskonsentrasjonen i oppgaven over?

Oppgave 3

Under sin ekspedisjon på FRAM (1893-1896) så observerte Nansen at isen drev til høyre (i Arktis) for vinden og han ba sin venn Vilhelm Bjerknes få en av sine studenter til å studere problemet. Det ble svensken Vagn Walfrid Ekman som forklarte isens bevegelse, som er et resultat av friksjon og jordens rotasjon. Ekman satte opp en teori for hvordan strømmen som vinden lager oppfører seg. Strømmen endrer seg med dypet (\(z\)) og vi kan skrive \(\vec{u(z)}=u(z)\vec{i} + v(z)\vec{j}\). Størrelsen på \(u(z)\) og \(v(z)\) kan vi beregne fra følgende formler (som ikke er så kompliserte som de ser ut!)

\(
u(z)=\frac{\sqrt{2}}{1000fd} e^{z/d}\left[\tau_x cos(z/d-\pi/4) -\tau_y sin(z/d-\pi/4)\right]
\)

 

\(
v(z)=\frac{\sqrt{2}}{1000fd} e^{z/d}\left[\tau_x sin(z/d-\pi/4) +\tau_y sin(z/d-\pi/4)\right]
\)

 

der \(z\) er høyde (så dybde er negativt), \(f=1.46\times10^{-4}sin(breddegrad)\) er Coriolis faktoren og \(d=\sqrt{\frac{2\nu}{\left|f\right|}}\) er tykkelsen på laget som kjenner vindens påvirkning. Vi kaller det ofte Ekman laget. \(\nu=10^{-2}m^2/s\) er viskositeten* – vannets “tykkelse” eller treghet (sirup har for eksempel en høyere viskositet enn vann **). Teorien er viden kjent blant oseanografer og kalles bare for “Ekman spiralen”.

* Den molekylære viskositeten til vann er mye lavere, \(\nu=10^{-6}m^2/s\), men i havet gjør virvler og turbulens at den effektive viskositeten blir større.

**Se for eksempel https://no.wikipedia.org/wiki/Viskositet for en animert illustrasjon av effekten av viskositet.

 

a) Hvilken verdi har Coriolis faktoren i Amundsenhavet? I Bergen?

b) Hvor tykt er Ekman laget? Et isfjell kan være fler hundre meter tykt – tror du det påvirkes av strømmen som vinden lager?

c) Om det blåser 15 m/s mot vest og det er isfritt, hvor stor er da \(\tau_x\) og \(\tau_y\)? (Se oppgave 2)

d) Fra hvilken retning (og med hvilken hastighet) flyter vannet i overflaten (z=0)? I Ekmandypet (z=-d)? På hvilket dyp går strømmen i motsatt retning av vinden?

e) Prøv å plotte strømmen! Hvorfor tror du vi snakker om Ekman spiral?

f) Når vi sender ned vår LADCP*** får vi strømprofiler med en oppløsning på 8 m (dvs vi får en verdi for strømmen for hver åttende meter). Tror du vi klarer å observere Ekman spiralen? Hvorfor/hvorfor ikke?

g) Når det blåser mot vest i Bergen, i hvilken retning går overflatestrømmen da?

*** Et instrument som følger med CTD’en ned til bunn og som måler strømmen i vannet på vei ned. Man får da strømprofiler i tillegg til profiler av salt og temperatur.

Oppgave 4

Om man summerer opp (integrerer) strømmen som vinden lager i Ekman laget så kan man regne ut transporten, dvs hvor mye vann som flyttes i en retning på grunn av vinden. Det kaller vi for Ekman transporten, \(\vec{Q_{Ekman}}=U\vec{i}+V\vec{j}\). Da får vi at

\(U=\frac{10^{-3}}{f}\tau_y\)

 

\(V=-\frac{10^{-3}}{f}\tau_x\)

 

Enheten på U og V er \(m^3/m/s\) (eller \(m^2/s\)) og de angir altså hvor mye vann som flyter forbi per meter per sekund. Uttrykket for \(\tau\) finner du i oppgave 2.

a) Om det blåser 15 m/s mot nordvest og det er isfritt, hvor stor er da U og V? I hvilken retning flyttes vannet?

b) Hvor stor er vinkelen mellom vinden og transporten?

c) Om vi har to bøyer (se figur under) som ligger 10 km i fra hverandre og der en linje mellom de to bøyene er parallell med vinden, hvor mye vann strømmer mellom bøyene på en time? Hva tror du skjer om linjen mellom A og B hadde vært kystlinjen?

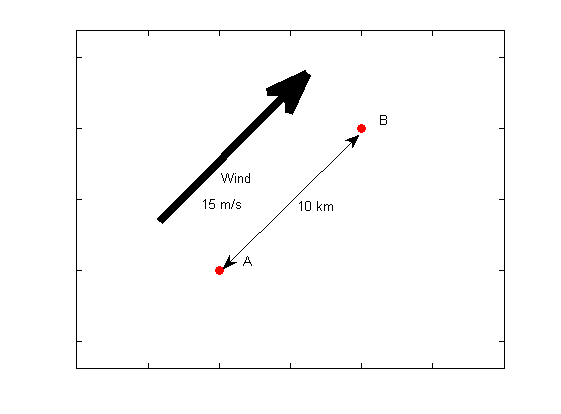
Når vinden blåser parallelt med kysten, kommer vannet enten til å samles opp mot kysten eller «forsvinne» fra kysten.

d) I hvilken retning tror du det blåser når vi får oversvømming på Bryggen i Bergen (tidevannet er selvsagt også viktig)?

e) Ved kysten av det Antarktiske kontinentet blåser vinden vanligvis mot vest. Lengre nord (60S) blåser det sterke vinder mot øst. Skisser hvordan vinden blåser og i hvilken retning Ekman transporten går. Hva tror du skjer i midten? Diskuter i grupper før dere leser svaret lenger nede på siden.

 

Konvergens og divergens i havet

Når vinden og dermed Ekman transporten har ulik retning (det holder egentlig at den endrer størrelse) fra ett område til et annet (som i oppgave 4) får vi “konvergens” (hvis overflatevann “samles sammen”, dvs. hvis pilene som viser Ekman transport peker mot hverandre) eller “divergens” (dvs. hvis pilene går fra hverandre). Når vi har divergens og overflatevannet “forsvinner” så må det etterfylles med vann nedenfra. Vann fra dypet “suges” opp til overflaten av vinden. I områder der dette skjer kontinuerlig (for eksempel rundt Antarktis) er det høy biologisk aktivitet ettersom vannet nede i dypet er rikt på næringsstoffer. Vindmønsteret rundt Antarktis løfter opp relativt tungt vann fra dypet og bidrar til vannet i den øvre delen av havet er tyngre enn i andre områder. Vann som har sunket til bunnen av Nord-Atlanteren kommer hit til overflaten igjen. For å lese mer, så kan du google f.eks ” wind driven upwelling “.